もっとも簡単なトランジスタ1石バッファー回路〜究極のナチュラルサウンドを求めて、その5

この記事では、バイポーラトランジスタ(BJT)たったの1石で作れる、もっも簡単なギターorベース用のバッファー回路を紹介します。
また、2SK30AなどによるFET版のバッファー回路や、オペアンプによるバッファー回路もございます。こちらの記事も合わせてご覧ください。
エミッタフォロワ回路
今回紹介するバッファー回路は、トランジスタによるエミッタフォロワ回路です。エミッタフォロワ回路について簡単に解説いたします。1石バッファー回路が早く見たい方は飛ばしてもらって構いません。
エミッタフォロワの基本回路
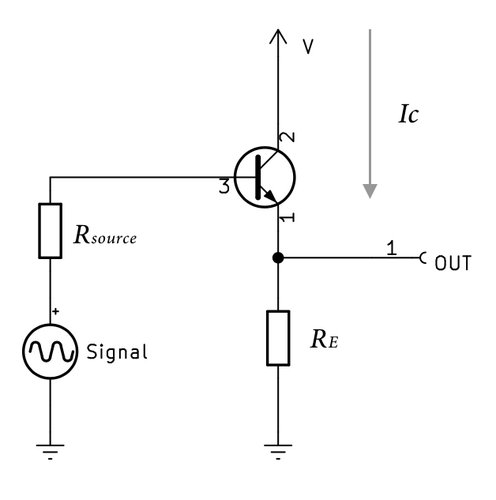
こちらは、トランジスタを使ったエミッタフォロワの基本回路図です。
トランジスタは一般にFETより入力インピーダンスが低いと言われますが、図に示すエミッタフォロワ回路であれば入力インピーダンスをかなり高くできることが分かりました。この回路ではコレクタが電源に落とされているので、交流的にはコレクタが接地されているとみなすことができます。ですのでエミッタフォロワ回路はコレクタ接地回路とも呼ばれてます。
エミッタフォロワ回路では、信号電圧の増幅はしません。そのかわり、電流の増幅を行うことができます。できるだけ元の波形を維持したまま、電流だけ大きくすることで外部ノイズに強くなったり、その後の機材入力で音質劣化しなくなったりとメリットがあるわけです。こういった役割をする回路を「バッファー回路」などと呼びます。
さて、この回路の入力インピーダンスと出力インピーダンスを計算したいのですが、なかなか計算方法が分かりませんでした。いろんな書籍を見ても、エミッタ接地回路ばかりで、コレクタ接地回路に関してあまり詳しく書かれてません。探し続けた結果、なんとWikipediaにインピーダンスの計算式が詳しく書かれていました。つぎでは、エミッタフォロワのインピーダンスを計算していきましょう。
▼ 参考サイト Common collector-Wikipedia Bipolar Transistor Cook book—Part2|Nuts & Volts Magazine
エミッタフォロワの入力インピーダンス
まずは、エミッタフォロワ回路の入力インピーダンスについてです。回路図を見ながら数式をご覧ください。
Wikipediaによれば、エミッタフォロワの入力インピーダンスは次式で近似されます。
$$Z_{IN} \approx βR_E \tag{1}$$ただし次の条件を満たすこと。
$$(g_mR_E \gg 1) \land (β \gg 1) \tag{2}$$βは交流信号における電流増幅値ですが、ここでは直流電流増幅値\(h_{FE}\)とほぼ同じであると考えることにします。 つまり、トランジスタの\(h_{FE}\)の値を、そのままβに代入します。
相互コンダクタンス
ところで、\(g_m\)とは相互コンダクタンス(ベースとエミッタ間の電圧変化に対するコレクタ電流変化の比)であり、次式で与えられます。
$$g_m=\frac{I_C}{V_T} \tag{3}$$さらに、\(V_T\)は熱電圧と呼ばれ、常温(27℃)では26mVであることが知られてます。
$$V_T=\frac{KT}{q}=26[mV] \tag{4}$$以上により、
$$g_m=\frac{I_C}{26\times10^{-3}} \tag{5}$$が導き出されます。 式2の条件を満たすよう、コレクタ電流\(I_c\)に気をつけましょう。
エミッタフォロワの出力インピーダンス
次に、エミッタフォロワの出力インピーダンスの計算式です。
エミッタフォロワの出力インピーダンスは、次式で近似されます。
$$Z_{OUT} \approx \frac{1}{g_m} + \frac{R_{source}}{β} \tag{6}$$ただし次の条件を満たします。
$$(β \gg 1) \land (Z_{IN} \gg R_{source}) \tag{7}$$\(R_{source}\)とは、テブナン等価なソース抵抗で、つまりは信号源の出力インピーダンスと考えられます。例えばギター(パッシブ)が信号源になるならば、ピックアップの出力インピーダンスと考えて200kΩ〜500kΩあたりになるでしょう。 \(R_{source}\)が大きくコレクタ電流も大きい場合、\(\frac{1}{g_m}\)はほとんど無視できる大きさとなります。 よって、式6を次のように簡略化できます。
$$Z_{OUT} \approx \frac{R_{source}}{β} \tag{8}$$ギターで使えるトランジスタ1石バッファー回路
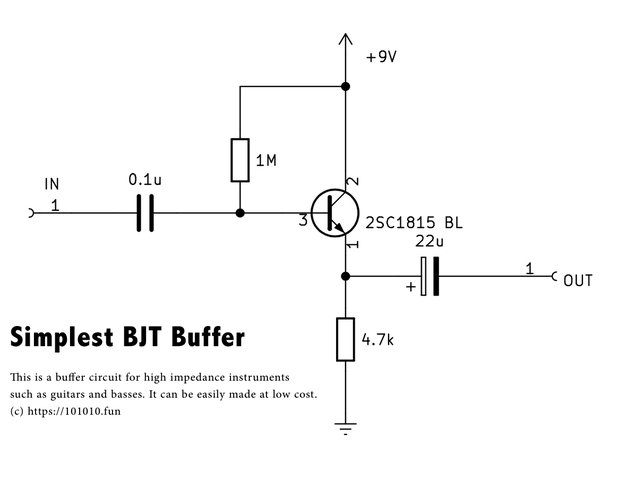
お待たせいたしました。こちらがギターで使えるトランジスタ1石バッファー回路です。
トランジスタは2SC1815のBLランクのものを使用しました。BLランクは\(h_{FE} (\approx β)\)が350〜700と高いため、今回の回路では入力インピーダンスを高くでき、そして出力インピーダンスを低くできます。 少量ですが手持ちのトランジスタをメルカリで販売してます。
hFEの測り方
トランジスタの直流電流増幅率\(h_{FE}\)の測り方はこちらの記事をご覧ください。
テスタ1つあればトランジスタの\(h_{FE}\)を測ることができます。または、最初からテスターに\(h_{FE}\)を測れる機能が付いているともっと便利です。ファミコンのようなデザインの測定器もございます。
インピーダンスを計算してみよう
さて、この回路の入力インピーダンスと出力インピーダンスを計算してみましょう。
先ほどの式1と式8をもう一度確認しましょう。
$$Z_{IN} \approx βR_E \tag{1}$$ $$Z_{OUT} \approx \frac{R_{source}}{β} \tag{8}$$ここでは、それぞれの値を次のように設定します。
| 項目 | 値 |
|---|---|
| \(β\) | 600 |
| \(R_E\) | 4.7kΩ |
| \(R_{source}\) | 220kΩ |
βの値は、1MΩを介してベース電流を与えたときのコレクタ電流を実測して計算した値です。\(h_{fe}\)は温度によって変化しますが、1mA程度のコレクタ電流であればトランジスタの発熱はないので問題ないでしょう。
\(R_{source}\)はギターのピックアップの出力インピーダンスを想定した値となります。
これらを元に、式1と式8に当てはめると次のように算出されました。
$$Z_{IN}=2.82[MΩ],~~Z_{OUT}=367[Ω]$$ここで回路図を見ると、入力にあるバイアス抵抗1MΩは交流的に接地されていると考えられます。よって、この抵抗も回路の入力インピーダンスの一部になります。\(Z_{IN}\)と1MΩの並列合成値が入力インピーダンスですので、1石バッファー回路のインピーダンスは次の表の通りです。
| 項目 | 値 |
|---|---|
| 入力インピーダンス | 740kΩ |
| 出力インピーダンス | 約400Ω |
| 消費電流 | 1mA(実測値) |
基板制作とモジュール化
1石バッファー回路を、基板を制作してモジュール化してみました。こうすることで、ブレッドボードで実験しやすくなります。

もっとも簡単なFET1石バッファー回路〜究極のナチュラルサウンドを求めて、その4 の回路よりも消費電流が大きくなりましたが、こちらのほうが出力インピーダンスは低くできているようです。出力インピーダンスが400Ωということは、マイク入力へ挿すことができるはずです。つまり、DI(アンバランスですが)として使うこともできますね!
性能測定
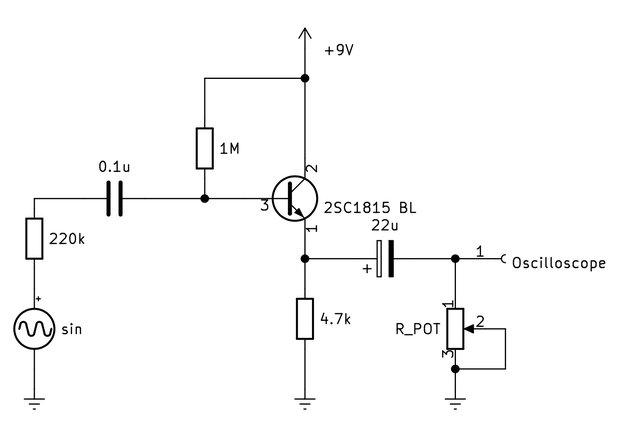
1石バッファー回路の性能を測定するため、図のような回路を組んでオシロスコープで波形を観察してみました。
ギターなどのハイインピーダンス楽器の入力をシミュレーションするため、発振器の出力後に220kΩの抵抗を入れてハイインピーダンス化しました。また、出力先のインピーダンスを自由に変えられるよう、負荷として可変抵抗を挟んでます。可変抵抗はディケイドボックスを使うと便利です。
▼ ディケイドボックスの自作も可能です。
オシロスコープで波形の観察
R_POTの負荷をどんどん低くすると、5kΩ以下から入力、出力信号ともに振幅が減少していきました。300Ωあたりで振幅がちょうど半分になります。しかし波形は歪まずに正弦波を保ってました。 一方、信号源の220kΩの抵抗を取り払い、ローインピーダンスの信号を入力してみたところ500Ω以下から出力波形の歪みが目立つようになりました。そして、150Ωあたりで信号源の半分の出力となります。 式8の通り、このエミッタフォロワバッファー回路では、信号源の出力インピーダンスによってバッファー回路自体の出力インピーダンスが変化してしまいます。ですので、用途によっては気をつけなければなりません。たいていの場合は、出力インピーダンス100〜500Ωの範囲です。
また、信号源の出力抵抗を700kΩにした時、入力信号の1/2の振幅が出力にあらわれました。よって、回路の入力インピーダンスは理論どおり、700kΩといえるでしょう。
以上、実験結果から1石バッファー回路のデータをまとめると次の通りです。
| 項目 | 値 |
|---|---|
| 入力インピーダンス | 700kΩ |
| 出力インピーダンス | 100〜500Ω |
| 消費電流 | 1mA |
発振器のすすめ
ところで発振器は、 クワドラチャ発振を使用しました。
こういった低周波の実験には「発振器」が一台あるとたいへん便利です。発振器は「ファンクションジェネレータ」や「オシレーター」とも呼ばれます。