エフェクターで使えるフィルタ回路|LPF・HPF・BPF
ローパスフィルタ(LPF)
オペアンプを使ったアクティブローパスフィルタの回路を紹介する。電源のいらないパッシブローパスフィルタは、どうしてもインピーダンスが高くなってしまい計算通りにフィルタがかからないことがある。しかしアクティブ回路なら安心だ。オペアンプを使うことで入力インピーダンスを十分に高くでき、出力インピーダンスを十分に下げられる。

今回は、ベースのエフェクタとして使えるように定数を設定した。必要であればギター用に改造することも難しくないはず。
ローパスフィルタとは
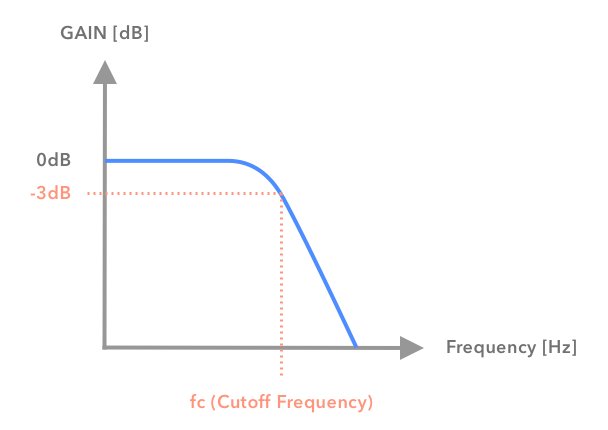
ローパスフィルタは簡単に言うと、高音をカットして低音だけ通すフィルターである。図のように、-3dB音量が下がる点fc[Hz]をカットオフ周波数と呼ぶ。
カットオフ周波数以降からだんだん音量が下がっていくのではなく、カットオフ周波数手前でも少し音量が下がっていることに注意。
ローパスフィルタはエフェクター意外にもさまざまな用途で使われているので覚えて損はない。ローパスフィルタを、思いっきりベースにかけるとモコモコして心地よい効果が得られる。ウッドベースやアコースティックベースの温もりのある音にも近いかもしれない。
回路図
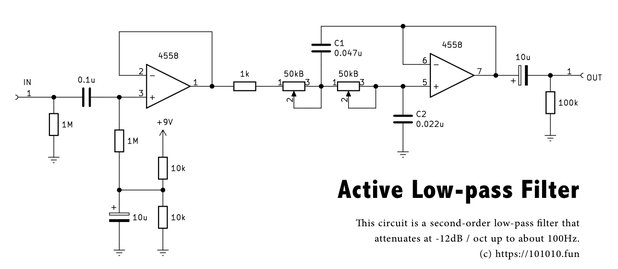
前段のオペアンプはバッファー回路となっており、ギターやベースを入力できるようにインピーダンス変換の役割をさせている。また、単一電源で動作させるため10kΩを2つ使ってバイアス電圧を作った。後段のオペアンプがメインのローパスフィルタ回路である。
カットオフ周波数の計算
この回路は2次のローパスフィルターとなっており、-12dB/octで高音が減衰していく。コンデンサの0.047μと0.022μがペアになっていて、二倍の関係になるように調節する。2つの容量の中間値をとって、次の公式よりカットオフ周波数を計算する。
$$ fc = \frac{1}{2πCR} $$つまり、0.047μと0.022μの中間値の0.035μFがCとなる。また可変抵抗を2連の50kΩに設定したので、Rを50kΩとして計算すると、最大カットオフ周波数はfc=91Hzとなった。

なお、高域はカットされるのでオペアンプには4558で十分だろう。
ハイパスフィルタ(HPF)
次にハイパスフィルタ版を紹介する。
回路図
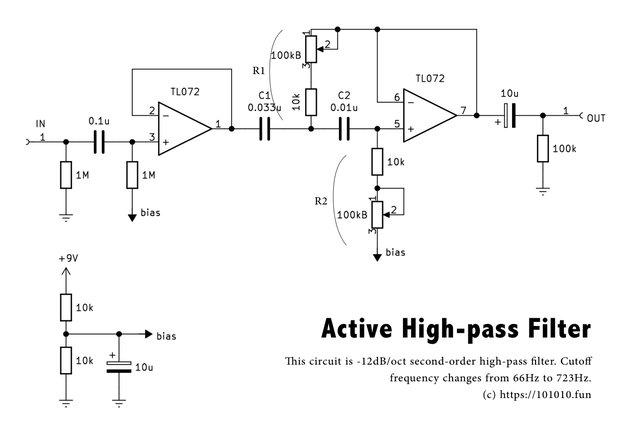
こちらがその回路図。2次のハイパスフィルタで、-12dB/0ctで減衰するバターワース特性を持つ。前段のオペアンプは、ハイインピーダンスの楽器を受けるためのバッファー回路。そして、後段がメインのハイパスフィルタ回路となる。
カットオフ周波数の計算
カットオフ周波数は次式で計算できる。
$$f_c=\frac{1}{2πCR}\tag{1}$$ただし、次の条件を満たすこと。
$$R=R1=R2, C1\simeq 1.4C , C2 \simeq \frac{C}{2}$$要するに、R1とR2を同じ値にして、C1とC2の半分の値をCとして式1に当てはめて計算すれば良い。回路図の定数では\(R=10kΩ〜110kΩ、C\simeq0.022u\)となるので、カットオフ周波数の範囲は66Hzあたりから723Hzまでとなる。 ギターで使いやすそうな周波数帯域に設定してある。また、カットオフ周波数をかなり低くできるようにしたので、マイクのローカットにも使える筈。

また、オペアンプはTL072を使用。ローパスフィルタの場合は高域がカットされるので4558で良かったが、ハイパスフィルタの場合はきらびやかさが売り。なので、高域の伸びの良いTL072がおすすめ。
ブリッジドT型バンドパスフィルタ(BPF)
最後にブリッジドT型バンドパスフィルタ回路を紹介する。バンドパスフィルタ回路を作るには色々あるかと思うが、その中でもブリッジドT型が一番簡単だったのでそれを紹介。
回路図
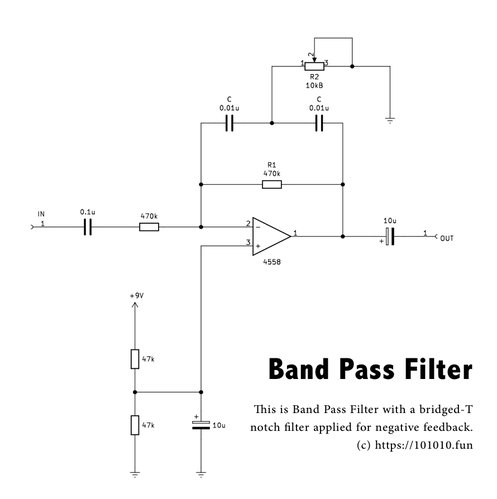
中心周波数の計算
中心周波数\(f\)は次の計算式で計算できる。
$$f=\frac{1}{2π\sqrt{\frac{R_1}{R2}}CR_2} \tag{1}$$また、この回路は反転増幅回路の応用なので470kΩの2つの抵抗で増幅率が決まる。ここでは同じ値にしているので、増幅率は1倍である。
ブリッジドT型バンドパスフィルタの伝達関数
次に、ブリッジドT型バンドパスフィルタの伝達関数\(H(s)\)を示す。
$$H(s)=\frac{R_1R_2C^2s^2+(2R_2+R_1)Cs+1}{R_1R_2C^2s^2+2R_2Cs+1} \tag{2}$$ノッチフィルタを不帰還しているため、ノッチフィルタの伝達関数\(G(s)\)の逆数を取れば\(H(s)\)が導き出される。
$$H(s)=\frac{1}{G(s)} \tag{3}$$よって、巷のノッチフィルタの伝達関数を参考に、式2を導き出した。
さて、この伝達関数\(H(s)\)を元にPythonで周波数特性をシミュレーションしてみた。つぎのプログラムでは、\(R_1=470kΩ、R_2=400Ω、C=0.01μF\)としたときの周波数特性をプロットする。
from control.matlab import *
import matplotlib.pyplot as plt
import numpy as np
if __name__ == '__main__':
R1 = 470 * pow(10, 3) # kΩ
R2 = 400 # Ω
C = 0.01 * pow(10, -6) # μF
fc = 1/(2*np.pi*C*R1)*np.sqrt(R1/R2)
print(fc)
H = tf([R1*R2*pow(C, 2), (2*R2 + R1)*C, 1], [R1*R2*pow(C,2), 2*R2*C, 1]) # 伝達関数
print(H)
W = logspace(1, 5) # 対数スケールの配列
bode(H, W, Hz=True)
plt.show()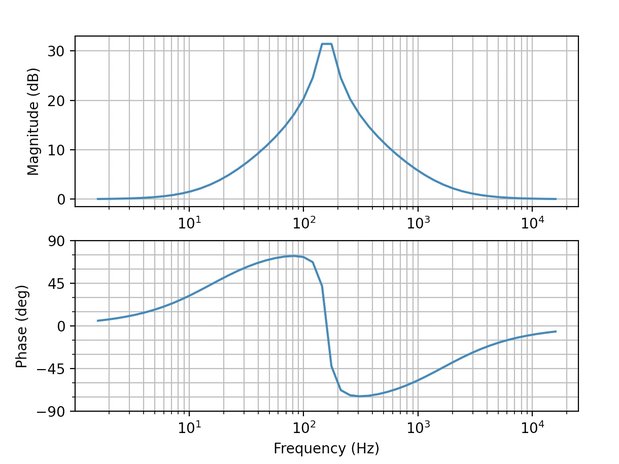
オペアンプで実験
次に、実際にオペアンプでTブリッジド型バンドパスフィルタ回路を組んで、ホワイトノイズをフィルタしてみた。ホワイトノイズの作り方は以下の記事を参考。
フィルタ回路の定数は、先ほどのシミュレーションと同様\(R_1=470kΩ、R_2=400Ω、C=0.01μF\)とした。
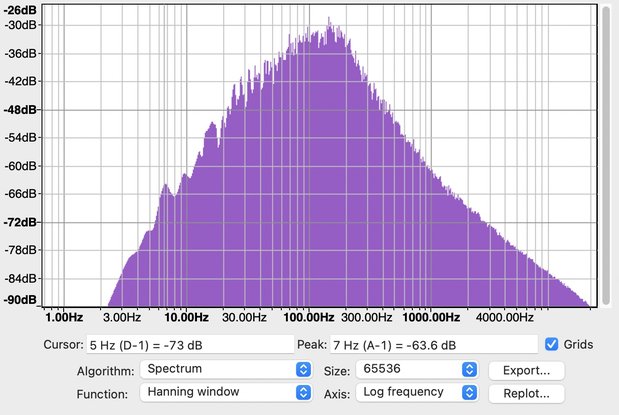
\(R_2\)を可変抵抗にすればこのように風のような音も作ることができる。ちなみにこの音源は、\(R_2\)を約10kΩから10Ωまで変化させた音である。 バンドパスフィルタとホワイトノイズがあるだけでかなり遊べるので、ぜひ作ってみてはいかがだろうか。 また、可変抵抗をフットペダルのボリューム抵抗に変えればオリジナルワウペダルを作ることも可能なはず。

さて、このモジュールを使って打楽器の音色を作ったり、擬似エンベロープと組み合わせてオートワウ効果を実験するとなかなか面白い。