ソースフォロワ(FET)の出力インピーダンス
FETの1石によるソースフォロワー(バッファー)回路の出力インピーダンスを調べてみました。相互コンダクタンスと呼ばれるgmの値を調べ、それを元に出力インピーダンスを計算します。また、分圧方による実際測定した出力インピーダンスとも比較します。
はじめに
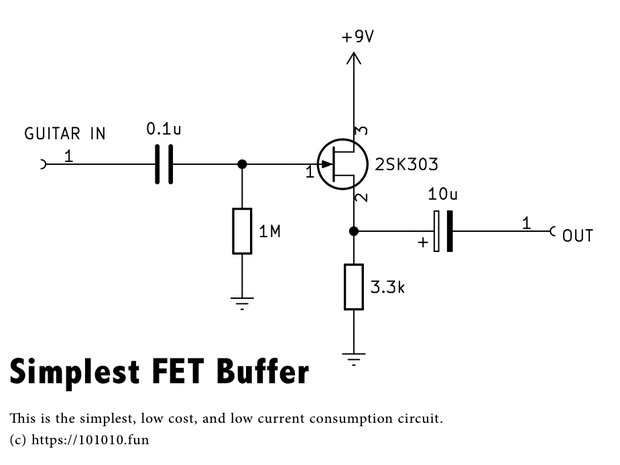
ギターやベースのエフェクターを製作していると次のような回路が頻繁に登場します。FETによるいわゆるソースフォロワーと呼ばれるバッファー回路です。ドレインが電源に直接繋がっているため、交流的には接地されていると考えることもできます。よってドレイン接地回路(Common drain)とも呼ばれています。
ギターなどのピックアップ出力はハイインピーダンス信号なため、ひ弱でノイズを拾いやすく音質劣化もしやすいです。そこでエフェクターの入力段には大抵このようなバッファー回路が設けらています。
これほどよく使われる理由としては、FETのゲート入力インピーダンスが非常に高いのが1つあります。回路図のように数個の抵抗とコンデンサを追加すれば、たったの一石のFETで気軽にバッファー回路が実現できます。
さてそんな中、入力インピーダンスが高いのは分かりますが、出力インピーダンスはいったいどれくらいなんだろうと疑問に思い調べることにしました。
トランジスタ回路はまだまだ未知な分野で勉強中ですが、少しでも知識がつけばと思い記事にアプトプットすることにします。ちなみに、私はこれらの書籍を参考書として勉強してきましたので紹介しておきます。
出力インピーダンスの計算式
FETのソースフォロワー(ドレイン接地)回路の出力インピーダンスですが、書籍を漁ってもFETに関しての情報に乏しく計算方法がわかりませんでした。そんな中、なんと Wikipediaに計算方法 が載ってましたのでそれを使うことにします。
その計算式がこちら。出力インピーダンス\(Z_{OUT}\)が計算できます。
$$Z_{OUT} = \frac{R_S}{g_{m}R_S+1} \tag{1}$$\(g_m\)は相互コンダクタンスと呼ばれるものです。相互コンダクタンスの単位はシーメンス[s]になります。ゲート電圧の変化量を\(ΔV_G\)としたときのドレイン電流の変化量を\(ΔI_D\)とすると、相互インダクタンスは次式で表されます。
$$g_m=\frac{ΔI_D}{ΔV_G} \tag{2}$$つまり、\(g_m\)は微分した値であり、あるグラフの傾きであると言えます。この相互コンダクタンスが大きい素子ほど、高い増幅率が得られると思って良さそうです。また、データシートによっては伝達アドミッタンス\(|Y_{fs}|\)と表記されますが、\(g_m\)と同じと考えて良いみたいです。
式1のRsはソースに繋がっている抵抗で、先ほどの回路だと3.3kΩがそれになります。
また、\(g_mR_S \gg 1\)であるならば、式1は次式で近似されます。
$$Z_{OUT}\approx \frac{1}{g_{m}} \tag{3}$$ですから\(g_{m}\)の値さえわかれば簡単に出力インピーダンスを計算できそうです。
ちなみに\(g_m\)は バイポーラトランジスタのエミッタフォロワのインピーダンス計算 にも出てきました。ですが、FETの場合は計算が全く異なりますので注意しましょう。
実際にgmを測定してみた
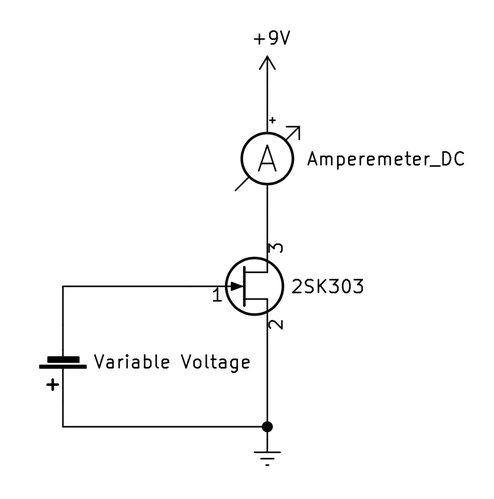
ここからは実際にFETの\(g_m\)を測定してみました。FETはNチャネルの2SK303を使用しました。 gm算出用の測定回路は次の図のように組みました。ゲートソース間に可変電源で電圧Vgsを掛けます。そのときにドレインに流れるドレイン電流Idを測定します。
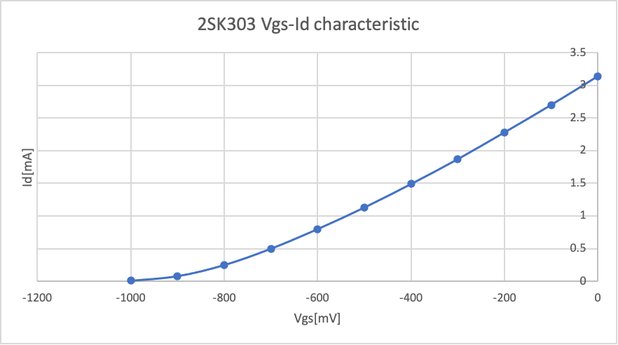
ところで2SK303はNチャネルですから、ゲートには負の電圧を掛けました。 2SK303のデータシート も参考になります。Vgsを100mV間隔で0V〜1Vまで可変させ、Idを測定した結果が次の表とグラフになります。
| Vgs [mV] | Id [mA] |
|---|---|
| 0 | 3.14 |
| -100 | 2.7 |
| -200 | 2.28 |
| -300 | 1.87 |
| -400 | 1.49 |
| -500 | 1.13 |
| -600 | 0.8 |
| -700 | 0.5 |
| -800 | 0.25 |
| -900 | 0.08 |
| -1000 | 0.01 |
直線性の良い-600mV〜0Vの値をもとに計算すると、\(g_m\)は3.9[ms]になります。計算するときはシーメンスの単位がミリであることに注意しましょう。 ちなみに、よくデータシートで見かける\(I_{DSS}\)は、ゲート電圧が0Vの時のドレイン電流のことです。このグラフでは\(I_{DSS}=3.14[mA]\)であることが分かります。
FET1石バッファーソースフォロワー回路の出力インピーダンス
はじめに最初に紹介したFETのソースフォロワー回路図です。こちらの出力インピーダンスを実際に計算してみます。このバッファーについては もっとも簡単なFET1石バッファー回路〜究極のナチュラルサウンドを求めて、その4 もご参考ください。
\(R_S=3.3[kΩ]\)、\(g_m=3.9[ms]\)として先ほどの式1に当てはめて計算すると、出力インピーダンス\(Z_{OUT}\)は238Ωとなりました。出力先に負荷抵抗をつけて分圧法で測定した場合は出力インピーダンスが800Ω程度ありましたので、随分と低い結果です。
ここら辺は今後の研究課題としてアップデートします。
オペアンプのボルテージフォロワーや、トランジスタのエミッターフォロワー回路の出力インピーダンスが100Ω以下であることを考えると、FETのソースフォロワー回路は出力インピーダンスがそれほど低くならないようです。実際に、10kΩ以上の負荷でないと波形が歪んでしまうことがありました。とは言えギターエフェクター用途では十分ではありますが。ソースフォロワー回路をDIとして、そのまま録音機材に突っ込むには注意が必要そうです。いやはや、FET回路も奥深いです♪