RCローパスフィルタのステップ応答
この記事では、ステップ入力によるRCローパスフィルタの過渡応答を計算していく。
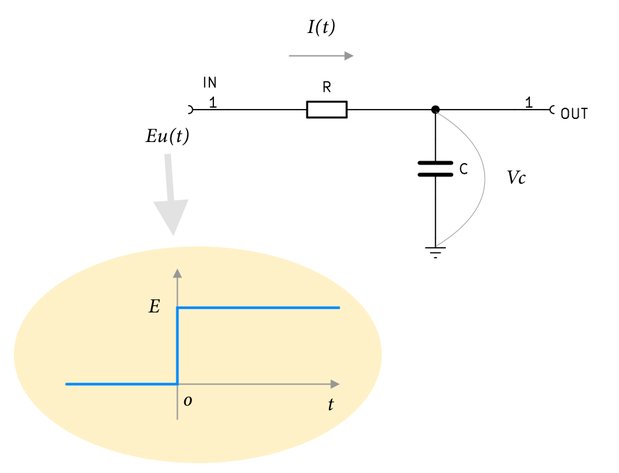
上の回路図のように抵抗Rと静電容量Cのコンデンサでローパスフィルタを組む。そしてこの回路に\(Eu(t)\)のステップ電圧を入力した時の出力電圧の様子を調べていく。
ステップ入力によるRCローパスフィルタの過渡応答
ステップ電圧は、\(t \geqq 0\)で電圧が\(E\)ボルトとなるような信号のことである。ちょうど\(t=0\)で、電圧のスイッチをオンにしたと思ってもらえれば良い。
また、出力電圧はコンデンサの両端の電圧\(V_c\)である。
ここで電圧\(V_c\)は
$$V_c(t)=\frac{q(t)}{C} \tag{1}$$である。
また、out端子につながる機材はハイインピーダンスであると考えて、電流はoutへほとんど流れないものとする。するとコンデンサに蓄えられる電気量の変化量が回路へ流れる電流と考えることができるので
$$\frac{dq(t)}{dt}=I(t) \tag{2}$$である。よって、
$$q(t)=\int I(t)dt \tag{3}$$となる。
式3を式1へ代入すると
$$V_c(t)=\frac{1}{C}\int I(t)dt \tag{4}$$が導き出される。
さて、ラプラス変換により電流\(I(t)\)は次の通り導き出される。この詳しい説明は前回記事を参考に。
$$I(t)=\frac{E}{R}e^{-\frac{1}{CR}t} \tag{5}$$式5を式4に代入すると
$$V_c(t)=\frac{1}{C}\int \frac{E}{R}e^{-\frac{1}{CR}t} dt \tag{6}$$である。
式7より式6は、
$$V_c(t)=\frac{E}{CR}(\frac{1}{-\frac{1}{CR}}e^{-\frac{1}{CR}t} + D) \tag{8}$$ $$V_c(t)=-Ee^{-\frac{1}{CR}t}+D \tag{10}$$となる。
\(\frac{E}{CR}D\)は定数なのでまとめてDと置き換えてしまう。すると式9は、
$$V_c(0)=-Ee^{-\frac{1}{CR}0}+D=0 \tag{11}$$となる。
ここでDについて考えてみよう。\(t=0\)の時、コンデンサの電圧は0Vであるから
$$D=E \tag{12}$$である。よって、
$$V_c(t)=-Ee^{-\frac{1}{CR}t}+E \tag{13}$$である。
式12を式10へ代入すれば
$$V_c(t)=E(1 - e^{-\frac{1}{CR}t}) \tag{14}$$となり、
$$V_c=E(1-e^{-1})$$となる。これがRCローパスフィルタにステップ入力したときの過渡応答である。
プログラミングでシミュレーション
せっかくなので式14をPythonでプログラミングしてプロットしてみよう。前回と同様に、Eを5V、Rを1kΩ、Cを1μFとしてシミュレーションしてみた。
前回の記事はこちら。
from matplotlib import pyplot as plt
import math
if __name__ == '__main__':
E = 5 # 5V
R = 1 * pow(10, 3) # 1kΩ
C = 1 * pow(10, -6) # 1uF
T = R * C # 時定数
sample = 1000
sec = 10 * pow(10, -3) # mS
times = [t * sec/sample for t in range(0, sample)]
Vc = []
for t in times:
Vc.append(E*(1-pow(math.e, -1/(C*R)*t)))
print("時定数: {}".format(T))
plt.figure(figsize=(16, 9), dpi=100)
plt.plot(times, Vc)
plt.title('Step Response RC LPF')
plt.xlabel('t[s]')
plt.ylabel('Vc[t]')
plt.legend()
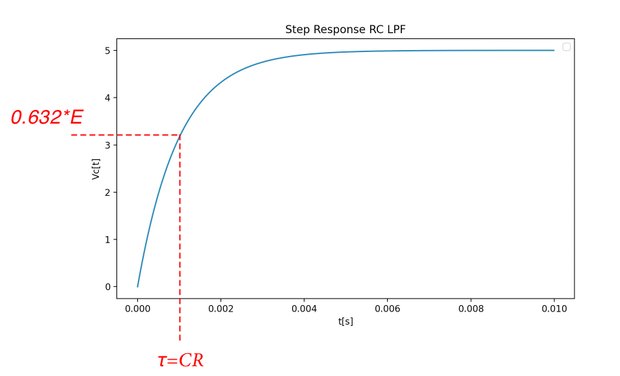
plt.show()プログラムの実行結果がこちら。ステップ入力の急激な変化がなだらかになった。つまり高周波成分がフィルターされたということである。
時定数
\(t=CR\)のとき
$$V_c=0.632E$$より、 $$V_c=0.632E$$ である。この時のCRを時定数τと呼ぶ。
この時定数を利用して、Arduinoでコンデンサの容量を測定してみた。
また、次の記事では伝達関数によるステップ応答を調べる方法を解説したので参考に。