はじめてのラプラス変換
この記事では、ラプラス変換の理屈は分からなくてもラプラス変換をとにかく使ってみようというテーマでお届けする。
電子回路に慣れ親しんでいる方なら、オペアンプの中身や仕組みが分からなくてもオペアンプを使うことはできるだろう。ラプラス変換も一緒で、ラプラス変換そのものの理屈は分からなくても、ラプラス変換を扱うことは高校生レベルの数学で可能なので安心を!
はじめに
ラプラス変換といえば制御工学で学ぶと思うが、教科書ではラプラス変換の仕組みから説明が入り、実際ラプラス変換のご利益に触れないまま工学分野を嫌いになってしまう方も多いのではないだろうか?実は私もその一人だ。
しかし、ラプラス変換を実際に使ってみるとこれが非常に面白い。いままで諦めていた微分方程式などもすらすら解けるようになるのだ。だからラプラス変換を知らないのは非常にもったいない。もう一度言おう。ラプラス変換することは高校生レベルの数学を学んでいれば誰でもできる。
そこでこの記事では、ラプラス変換の難しい説明をできるだけ省き、とにかく手を動かしてラプラス変換を使ってその利便性に触れることを目的として進めていく。
ラプラス変換とは
ラプラス変換をとにかく使ってみよう!
とはいえ、使う上で大体のイメージは必要である。
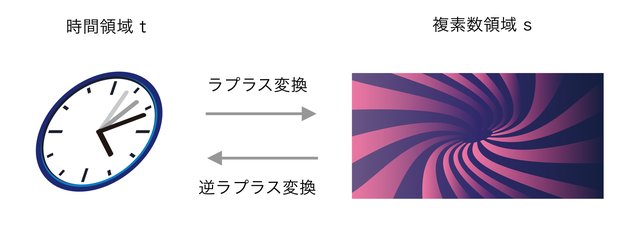
ラプラス変換とは、時間領域tの関数を複素数領域sへと置き換えて、微分・積分などの演算を簡単にするための手法である。
さっそく、複素数領域だとかなんのこっちゃ分からないかもしれないが、大事なのは、微積分の面倒な計算を足し算に置き換えてくれる超便利なツールであるということ。 複素数が分からなくてもラプラス変換は使えるので安心してもらって良い。
実は、電気回路や制御工学などでは解に微分・積分が多く含まれてしまうため、ラプラス変換することで足し算・割り算レベルの簡単な数式に置き換えられるメリットがあるのだ。
しかも、ラプラス変換はすでに用意されている変換表と照らし合わせて変換すれば良いだけなので何も難しいことはない。
作業手順としては次のような流れになる。
- 時間関数f(t)を組み立てる
- ラプラス変換する
- s領域で計算する
- 逆ラプラス変換して再び時間領域tへ戻す
ラプラス変換された関数は複素数領域の関数であるため、そのままでは現実世界に適応できない。そこで、再び時間領域へ戻すために逆ラプラス変換が必要である。しかしこの逆ラプラス変換というのも、変換表通りやれば高校生レベルでできる話なので安心して良い。
それでは、ラプラス変換対応表を見ていくことにしよう。
ラプラス変換対応表
下の表が、ラプラス変換対応表である。時間領域tの関数を複素数領域sへ置き換えることがラプラス変換である。sがなんのこっちゃ分からなくても、とにかく時間tをsの関数に置き換えるにはこの表に当てはめて変換すれば良い。
この表を使えば、複素数領域sから時間領域tへ置き換えること(逆ラプラス変換)も簡単にできる。
| $$f(t)$$ | $$F(s)$$ | 説明 |
|---|---|---|
| $$δ(t)$$ | $$1$$ | 単位インパルス関数$$δ(t)=\begin{cases}\infty~(t=0)\\0~~~(t\neq0)\end{cases}$$ |
| $$u(t)$$ | $$\frac{1}{s}$$ | 単位ステップ関数$$u(t)=\begin{cases} 0~(t \lt 0) \\ 1~(t \geqq 0) \end{cases}$$ |
| $$e^{-at}$$ | $$\frac{1}{s+a}$$ | 指数関数 |
| $$sin(ωt)$$ | $$\frac{ω}{s^2+ω^2}$$ | 三角関数(正弦) |
| $$cos(ωt)$$ | $$\frac{s}{s^2+ω^2}$$ | 三角関数(余弦) |
| $$f'(x)$$ | $$sF(s)-f(0)$$ | 微分 |
| $$f''(x)$$ | $$s^2F(s)-sf(0)-f'(0)$$ | 二階微分 |
| $$\int_0^tf(τ)dτ$$ | $$\frac{1}{s}F(s)$$ | 積分 |
この記事では、上記の表の単位ステップ関数 指数関数 積分だけを使うので、今これらの全部の変換を覚える必要はない。
指数関数と積分の説明は、高校の授業で習ったので大丈夫だろう。単位ステップ関数については、図のように0秒以降から1となる関数である。実はこれ、\(t \geqq 0\)で1V電源のスイッチをオンにしたようなものだと思って構わない。そんな関数を単位ステップ関数と呼ぶ。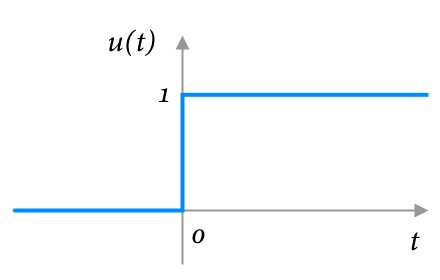
それでは、これらの変換表と照らし合わせながら現実世界の現象をラプラス変換してみようと思う。具体的には、電子回路のRC直列回路を使ってラプラス変換・逆ラプラス変換を実践していくことにする。
RC直列回路の時間関数
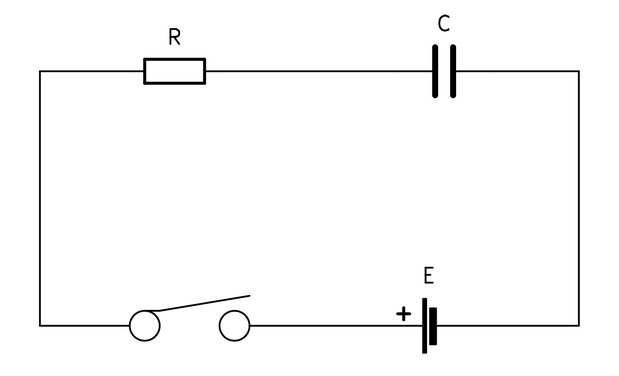
図のようなRC直列回路で考えてみよう。ある時間\(t=0\)でスイッチをオンにした時の電流の流れ具合(過渡応答特性)を考えてみる。先ほど伝えたとおり、スイッチをオンにするということは、単位ステップ関数を入力するのと非常によく似ていることを頭の片隅に置いといてもらいたい。
さて、これから説明することは高校生の物理を習っていればスムーズに理解できると思う。
抵抗Rに掛かる電圧は、
$$V_R(t)=RI(t) \tag{1}$$である。また、コンデンサに掛かる電圧は、
$$V_C(t)=\frac{1}{C}\int I(t)dt \tag{2}$$である。よって、キルヒホッフの法則から\(V(t)=V_R(t)+V_C(t)\)なので
$$V(t)=RI(t)+\frac{1}{C}\int I(t)dt \tag{3}$$が成り立つ。
ここで\(t \geqq 0\)で電源スイッチをオンにして、\(E\)の電圧を回路へ掛けてみよう。
と考えることができる。
よって、式3は
$$Eu(t)=RI(t)+\frac{1}{C}\int I(t)dt \tag{5}$$と書き換えることができる。これで、RC直列回路にステップ電圧を入力した時の関数を作ることができた。
しかし、この式には積分が含まれているのでとても計算しづらい。そこで、ラプラス変換の登場だ。次では、式5をもっと簡単な数式で表現できるようにするためラプラス変換を行なっていく。しつこいが、ラプラス変換は対応表に照らし合わせればなにも難しいことはないので安心してもらって良い。
RC直列回路のラプラス変換
それでは、式5を対応表をみながらラプラス変換してみよう。
積分と単位ステップ関数のラプラス変換の関係は次の通りであった。
| $$f(t)$$ | $$F(s)$$ |
|---|---|
| $$\int_0^tf(τ)dτ$$ | $$\frac{1}{s}F(s)$$ |
| $$u(t)$$ | $$\frac{1}{s}$$ |
よって、式5をラプラス変換すると
$$\frac{E}{s}=RI(s)+\frac{1}{sC}I(s) \tag{7}$$と置き換えることができる。
式7を電流について展開すると
$$I(s)=\frac{E}{s(R+\frac{1}{sC})} \tag{8}$$ $$I(s)=\frac{E}{SR+\frac{1}{C}} \tag{9}$$ $$I(s)=\frac{E}{R}\frac{1}{s+\frac{1}{CR}} \tag{10}$$となる。
RC直列回路の逆ラプラス変換
さて、式10をよく見るとラプラス変換における指数関数の対応関係になっているのがお分かりだろうか。つまり、下の表の\(a\)に相当するのが、式10では\(\frac{1}{CR}\)である。
| $$f(t)$$ | $$F(s)$$ |
|---|---|
| $$e^{-at}$$ | $$\frac{1}{s+a}$$ |
だから、式10を逆ラプラス変換すると
$$I(t)=\frac{E}{R}e^{-\frac{1}{CR}t} \tag{12}$$となる。
ラプラス変換して計算し、さらに逆ラプラス変換することで積分が含まれない簡単な式となった。これがラプラス変換というツールを使うメリットである。
ちなみに式12は、ステップ入力Eを掛けた時のRC直列回路における電流のステップ応答(過渡現象)に他ならない。
ラプラス変換記号
ここまでの説明を理解できた方なら、もう次のラプラス記号の意味はお分かりであろう。ラプラス変換と逆ラプラス変換をこのように書きますよというだけのことである。
$$F(s) = \mathcal{L}[f(t)]$$$$f(t) = \mathcal{L}^{-1}[F(s)]$$
また、定数はラプラス変換しても定数のまま引き継げる。
Pythonでグラフを描いてみよう
せっかくなので、ラプラス変換により導き出された式12をPythonでプログラミングしてみよう。次のプログラムは電流と時間の関係をグラフ化するものである。ここではEを5Vとし、Rを1kΩ、Cを1μFとしてシミュレーションしてみた。
from matplotlib import pyplot as plt
import math
if __name__ == '__main__':
E = 5 # 5V
R = 1 * pow(10, 3) # 1kΩ
C = 1 * pow(10, -6) # 1uF
T = R * C # 時定数
sample = 1000
sec = 10 * pow(10, -3) # mS
times = [t * sec/sample for t in range(0, sample)]
I = []
for t in times:
I.append(E / R * pow(math.e, -1/C/R*t))
print("時定数: {}".format(T))
plt.figure(figsize=(16, 9), dpi=100)
plt.plot(times, I)
plt.title('RC Series Circuit')
plt.xlabel('t[s]')
plt.ylabel('I[t]')
plt.legend()
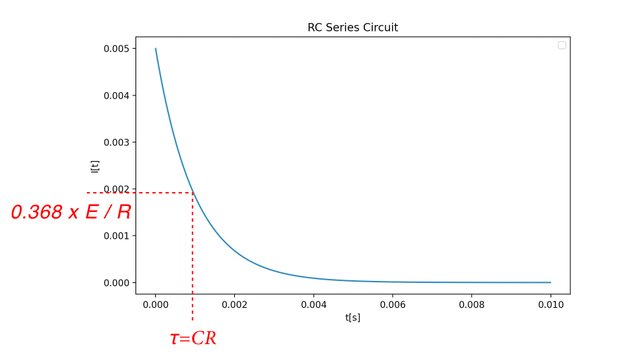
plt.show()RC直列回路では、コンデンサに電荷が溜まっていくにつれ電流が流れにくくなるので、このようなグラフになるのも頷けると思う。
なお、\(t=CR\)のときの時間を時定数と呼び\(τ\)で表す。 式12へ、\(t=CR\)を代入すればわかる通り、この時の電流の値は\(0.368 \times \frac{E}{R}\)となる。
時定数の性質を使って、Arduinoでコンデンサの容量を測定してみた。