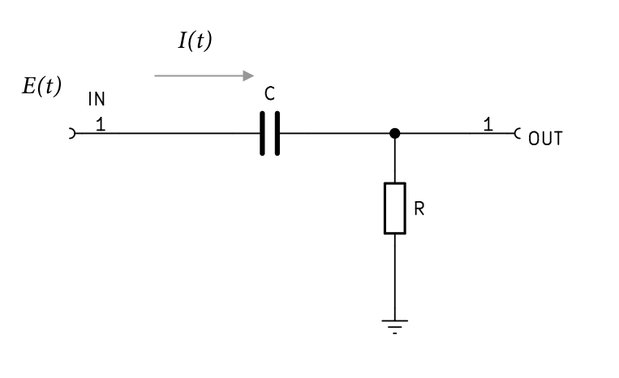
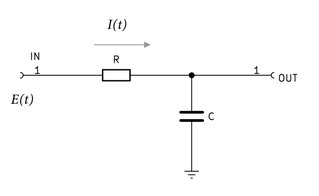
デジタル信号におけるRCハイパスフィルタ
デジタル信号におけるRCハイパスフィルタは次の式となる。
$$y_i=ay_{i-1}+a(x_i-x_{i-1}) \tag{1}$$なぜこの式がRCハイパスフィルタになるのか、ここで詳しく解説してみたいと思う。
基本的にローパスフィルタの記事で説明した方法と同じやり方でハイパスフィルタは導き出すことができる。
はじめに
本記事を書くにあたって参考になった本をご紹介します。
こちらの書籍はデジタルフィルタに関して、プログラミング例とともに解説されてます。FIRやIIRといった実用的なデジタルフィルタを実際に使うことができるのでおすすめです。アナログ回路のRCハイパスフィルタ
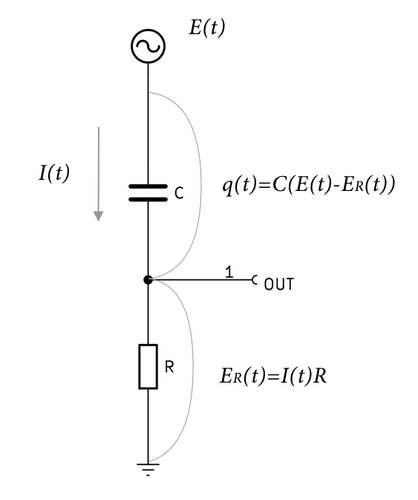
電圧を分かりやすくするために最初の回路図を少し変形させた。
回路図より、
$$E_R(t)=I(t)R \tag{1}$$である。 また、
$$q(t)=CE_C=C(E(t)-E_R(t)) \tag{2}$$ $$E_R(t)=\frac{dq(t)}{dt}R=C(\frac{dE(t)}{dt}-\frac{dE_R(t)}{dt})R\tag{4}$$なので、式1は
$$E_R(t)=RC(\frac{dE(t)}{dt}-\frac{dE_R(t)}{dt})\tag{5}$$となる。よって出力電圧\(E_R(t)\)は次式で導き出される。
$$y_i=RC(\frac{x_i-x_{i-1}}{ΔT}-\frac{y_i-y_{i-1}}{ΔT}) \tag{6}$$電圧をデジタルデータで考える
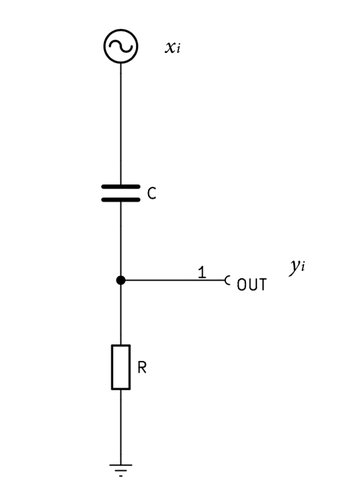
ここで、電圧をサンプリングデータに置き換える。\(E(t)\)を\(x_i\)とし、\(E_R(t)\)を\(y_i\)とすると、式5は次のようになる。ただし、\(ΔT\)はサンプリング周期である。
$$y_i=\frac{RC}{RC+ΔT}y_{i-1}+\frac{RC}{RC+ΔT}(x_i-x_{i-1})\tag{7}$$さて、式6を\(y_i\)について解くと、
$$y_i=ay_{i-1}+a(x_i-x_{i-1}) \tag{8}$$となる。
ここで\(a=\frac{RC}{RC+ΔT}\)に置き換えると、
$$a=\frac{RC}{RC+ΔT}\tag{9}$$となり、RCハイパスフィルタのデジタルフィルタ計算式が導き出された。
カットオフ周波数
最後にカットオフ周波数と\(a\)の関係を導き出してみよう。
係数\(a\)は、
$$f_c=\frac{1}{2πRC}\tag{10}$$であった。 また、RC回路におけるカットオフ周波数\(f_c\)は次式で求められる。
$$RC=\frac{1}{2πf_c}\tag{11}$$これを展開すると、
$$a=\frac{1}{2πΔTf_c+1} \tag{12}$$となる。式11を式9へ代入して係数\(a\)について展開すれば、 $$a=\frac{1}{2πΔTf_c+1} \tag{12}$$ の関係となる。