デジタル信号におけるRCローパスフィルタ
デジタル信号におけるRCローパスフィルタは次の式となる。
$$y_i=ax_i+(1-a)y_{i-1} \tag{1}$$なぜこの式がRCローパスフィルタになるのか、ここで詳しく解説してみたいと思う。
はじめに
本記事を書くにあたって参考になった本をご紹介します。
こちらの書籍はデジタルフィルタに関して、プログラミング例とともに解説されてます。FIRやIIRといった実用的なデジタルフィルタを実際に使うことができるのでおすすめです。アナログ回路のRCローパスフィルタ
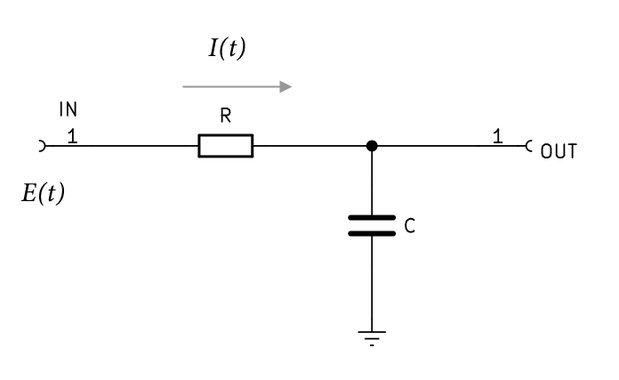
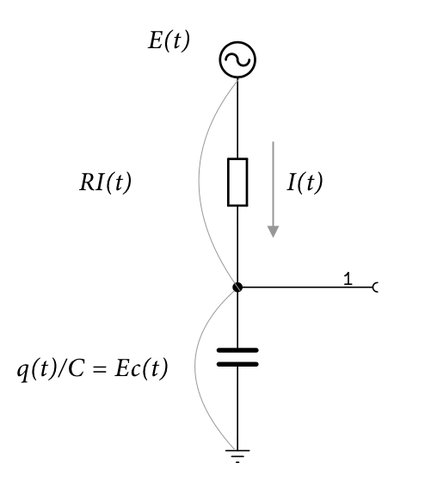
話を分かりやすくするために、最初の回路図を少し変形させてみよう。
信号源を\(E(t)\)とし、時間\(t\)によって信号の電圧は変化する。
抵抗\(R\)に流れる電流は\(I(t)\)なので、抵抗の両端にかかる電圧は\(RI(t)\)である。また、コンデンサの電圧は\(Ec(t)\)とすると、\(Ec(t)=\frac{q(t)}{C}\)が成り立つ。
よって、キルヒホッフの法則より、
$$E(t)=RI(t)+\frac{q(t)}{C} \tag{2}$$となる。
また、ある時間における電流\(I(t)\)はコンデンサの電気量\(q\)の変化量であるから
$$I(t)=\frac{dq(t)}{dt} \tag{3}$$で表せる。 ここでポイントなのは、図のOUT端子(抵抗とコンデンサの間)へ接続される負荷はハイインピーダンスであるため、出力端子へほとんど電流が流れていかないものとしている。
式3を式2へ代入すると、
$$E(t)=R\frac{dq(t)}{dt}+\frac{q(t)}{C}\tag{4}$$となる。
コンデンサの電圧は\(CE_c(t)=q(t)\)なので
$$E_c(t)=\frac{q(t)}{C}\tag{5}$$である。式5を式4へ代入すると、
$$RC\frac{dE_c(t)}{dt}+E_c(t)=E(t)\tag{6}$$である。
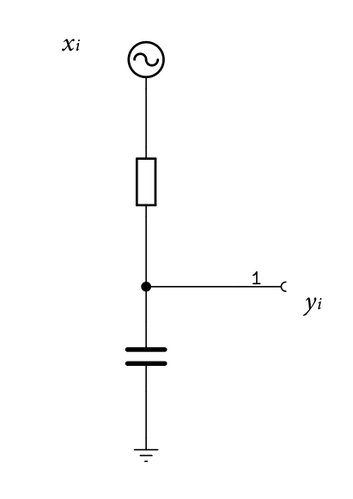
電圧をデジタルデータで考える
ここで、電圧をデジタルのサンプリングデータとして考えると\(x_i=E(t)\)、\(y_i=E_c(t)\)で置き換えることができる。
よって、式6は次のようになる。ただし\(ΔT\)はサンプリング周期である。
$$RC\frac{y_i-y_{i-1}}{ΔT}+y_i=x_i\tag{7}$$これを\(y_i\)について解くと、
$$y_i=\frac{ΔT}{RC+ΔT}x_i+\frac{RC}{RC+ΔT}y_{i-1}\tag{8}$$となる。 また、
$$\frac{RC}{RC+ΔT}=\frac{ΔT-ΔT+RC}{RC+ΔT}=\frac{RC+ΔT}{RC+ΔT}-\frac{ΔT}{RC+ΔT}$$なので、ここで\(a=\frac{ΔT}{RC+ΔT}\)とおけば、式8は
$$y_i=ax_i+(1-a)y_{i-1}\tag{9}$$となり、デジタル信号におけるRCローパスフィルタが導き出された。
カットオフ周波数
最後にカットオフ周波数と\(a\)の関係を導き出してみよう。
係数\(a\)は、
$$a=\frac{ΔT}{RC+ΔT}\tag{10}$$であった。 また、RC回路におけるカットオフ周波数\(f_c\)は次式で求められる。
$$f_c=\frac{1}{2πRC}\tag{11}$$これを展開すると、
$$RC=\frac{1}{2πf_c}\tag{12}$$となる。式12を式10へ代入して計算すれば、
$$a=\frac{2πΔTf_c}{2πΔTf_c+1}\tag{13}$$の関係が導き出される。