LRローパスフィルタの伝達関数

ステップ応答についてはこちらで詳しく解説したので参考に。
はじめに
本記事を書くにあたって参考になった書籍をご紹介します。
LRローパスフィルタの伝達関数
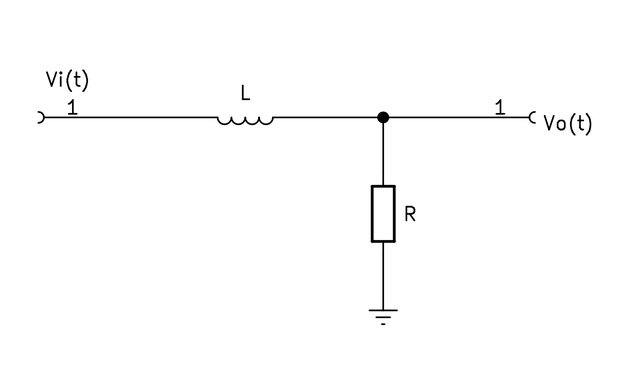
である。また、出力先の入力インピーダンスを無限大とすれば
$$i(t)=\frac{v_o(t)}{R} \tag{2}$$である。式2を式1へ代入すると、
$$v_i(t)=\frac{L}{R}\frac{dv_o(t)}{dt}+v_o(t) \tag{3}$$が成り立つ。ここで\(v_i(0)=0,~v_o(0)=0\)とし、両辺をラプラス変換すると
$$V_i(s)=\frac{Ls}{R}V_o(s)+V_o(s) \tag{4}$$となり、伝達関数は
$$H(s)=\frac{V_o(s)}{V_i(s)}=\frac{1}{\frac{L}{R}s+1}=\frac{\frac{R}{L}}{s+\frac{R}{L}} \tag{5}$$である。また、時定数は
$$τ=\frac{L}{R} \tag{6}$$であり、カットオフ周波数は
$$f_c=\frac{R}{2πL} \tag{7}$$である。
Pythonで周波数特性とステップ応答
伝達関数が求められたところで、Pythonで周波数特性とステップ応答を調べてみよう。コイルのインダクタンスLを1000uHとし、Rを1kΩとした。
from control.matlab import *
import matplotlib.pyplot as plt
import numpy as np
if __name__ == '__main__':
R = 1000
L = 1000 * pow(10, -6) # uH
T = L / R
print(T)
fc = R / (2 * np.pi * L)
print(fc)
G = tf([0, 1], [T, 1]) # 伝達関数
print(G)
W = logspace(4, 8) # 対数スケールの配列
bode(G, W, Hz=True)
plt.show()
y, t = step(G, np.arange(0, 0.00001, 0.0000001)) # ステップ応答
plt.plot(t, y)
plt.legend()
plt.show()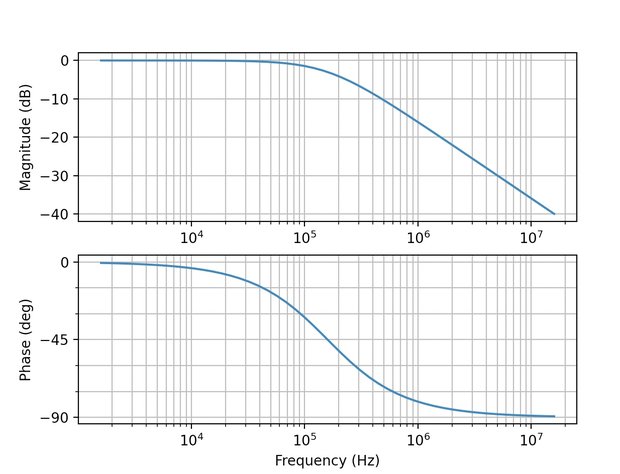
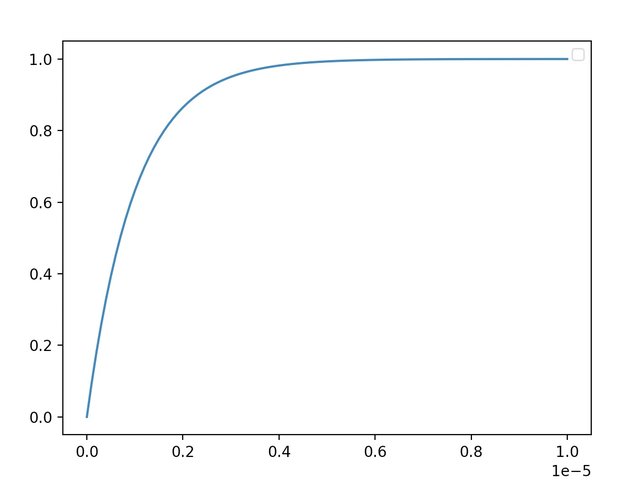
しかし、Arduinoの分解能が4μS程度なので時定数が1μSとなるコイルのインダクタンス測定は厳しい。また、例えば5Vのステップ電圧をかけた時の電流は\(I=\frac{V}{R}\)より、最終的に5mAの電流が流れる事になる。抵抗Rを1kΩ以下に小さくして、電流を多く流せば時定数は大きくなるが、今度はArduinoの出力電流許容範囲(20mA程度)を超えてしまう。また、MOSFETを使って大電流を流す方法も考えられるが、そうするとコイルに磁性が帯びて性能面で問題が出てしまうかもしれない。 もちろん、コイルのインダクタンスがもっと大きい場合はArduinoでも測定可能であろう。