Pythonで組み合わせの計算を高速で処理するアルゴリズム
写真の機材は、さまざまな静電容量を作ることができる「Capacitance Decade Box」だ。スイッチが35個ある。コンデンサを並列に繋いでいるため、色々な容量を足し算で作り出せるわけだ。 それでは一体、どれほどのパターンの静電容量を作り出すことができるだろうか?そんなことに、興味が沸いた。この記事では、Pythonを使ってこの35個のスイッチの組み合わせが何通りあるかを計算してみた。
nの階乗の計算 (factorial)
まず、nの階乗から計算してみよう。 nの階乗は、
$$(n - ( n - 1 ) ) \times (n - ( n - 2 ) ) \times (n - ( n - 3 ) ) ... \times (n - ( n - n ) )$$と書くことができる。
たとえば、nが4の場合
$$ (4 - (4 - 1 ) ) \times (4 - ( 4 - 2 ) ) \times (4 - ( 4 - 3 ) ) \times (4 - ( 4 - 4 ) )$$となる。 実際に計算してみれば、24となり正しい値となった。
$$1 \times 2 \times 3 \times 4 = 24$$この計算式を、factorial関数として定義しておこう。ただし、n = 0の階乗は1とする。
def factorial(n):
res = 1
for i in range(1, n + 1):
res *= i
return res
print(factorial(4)) 24が出力された。
ちなみに、階乗の計算はmathモジュールのfactorialを使って計算できる。しかし、他のプログラミングへ移植することもあるので、このように1から作って損はない。
組み合わせの計算 (combination)
次に、組み合わせの計算を行う。
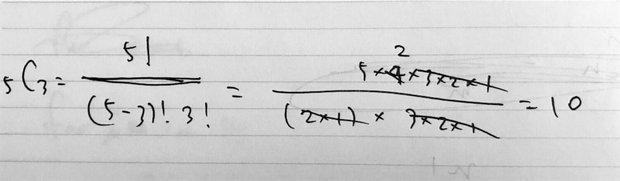
$$ {}_n C_r = \frac{n!} {(n-r)! r!}$$先ほど作ったfactorial関数を利用すれば、組み合わせの計算も簡単にできる。ビックリマークの階乗をすべてfactorialに置き換えれば良いだけ。 たとえば、 n = 5 、 r = 3の場合を考えてみよう。プログラムは次の通り。計算結果は10.0となるはずだ。
n = 5
r = 3
result = factorial(n) / (factorial(n - r) * factorial(r))
print(result)実際に手書きでも計算してみたところ計算間違いはなさそうなので、この組み合わせのアルゴリズムをcombination関数として定義した。
def combination(n, r):
return factorial(n) / (factorial(n - r) * factorial(r))35個の中から選ぶ組み合わせ

n = 35
total = 0
for r in range(1, n+1):
res = combination(n, r)
print("{n}C{r} = {res}".format(
n=n,
r=r,
res=res))
total += res
print("合計:", total)出力結果はこちら。
35C1 = 35
35C2 = 595
35C3 = 6545
35C4 = 52360
35C5 = 324632
35C6 = 1623160
35C7 = 6724520
35C8 = 23535820
35C9 = 70607460
35C10 = 183579396
35C11 = 417225900
35C12 = 834451800
35C13 = 1476337800
35C14 = 2319959400
35C15 = 3247943160
35C16 = 4059928950
35C17 = 4537567650
35C18 = 4537567650
35C19 = 4059928950
35C20 = 3247943160
35C21 = 2319959400
35C22 = 1476337800
35C23 = 834451800
35C24 = 417225900
35C25 = 183579396
35C26 = 70607460
35C27 = 23535820
35C28 = 6724520
35C29 = 1623160
35C30 = 324632
35C31 = 52360
35C32 = 6545
35C33 = 595
35C34 = 35
35C35 = 1
合計: 34359738367ななななんと!、たった35種類のコンデンサから並列合成して343億通りもの静電容量を作り出すことができることが分かった。もちろん順列ではない、組み合わせでだ。最初は計算間違ではないかと疑ったが、どうも本当らしい。
ちなみに、組み合わせを配列で返してくれる関数も作ってみたので紹介しておく。
def nCr(s1, r): # ただしmは、1 <= m <= len(s1) の範囲とする
a = s1[0] # 配列の最初の値を対象する
# a と組み合わせられる値は aを以外の配列を対象とすれば良い
s2 = s1[1:] # => [2, 3, 4, 5]
res = []
if r == 1: # 例外ケースとして処理
for a in s1:
res.append(a)
return res
elif r == 2:
for b in s2:
res.append([a, b])
else:
for bc in nCr(s2, r-1):
# bc.insert(0, a)
bc.append(a)
res.append(bc)
if len(s1) > r - 1:
return res + nCr(s2, r)
else:
return []あとから知ったが、Pythonには itertools.combinations で組み合わせを計算できる。私が作ったプログラミングは多少スペックは落ちる。配列処理がボトルネックになっている。35C17を計算した場合、40億を超える配列を処理しなければならない。 nCrは再帰処理なので、それならばキャッシュを使ったらかなり速度改善できそうだ。そんなわけで、先ほどのプログラムにキャッシュを導入して改善してみた。
cache = {}
def join(a):
s = ""
for b in a:
s += str(b) + "_"
return s
def nCr(s1, r): # ただしmは、1 <= m <= len(s1) の範囲とする
a = s1[0] # 配列の最初の値を対象する
# a と組み合わせられる値は aを以外の配列を対象とすれば良い
s2 = s1[1:] # => [2, 3, 4, 5]
res = []
if r == 1: # 例外ケースとして処理
for a in s1:
res.append(a)
return res
elif r == 2:
for b in s2:
res.append([a, b])
else:
for bc in nCr(s2, r-1):
# bc.insert(0, a)
bc.append(a)
res.append(bc)
if len(s1) > r - 1:
prefix = join(s2)
key = "{prefix}{n}C{r}".format(prefix=prefix, n=len(s2), r=r)
if cache.get(key) is None:
cache[key] = nCr(s2, r)
return res + cache[key]
else:
return []キャッシュを利用すると速い。なかなか悪くない結果が得られたのでベンチマークをとってみた。 35C1から35C9までを計算した結果である。キャッシュの差がじわじわ効いている。
| itertools.combinations | nCr (キャッシュ版) | |
|---|---|---|
| 1回目 | 71.492s | 27.765s |
| 2回目 | 70.68s | 28.093s |
| 3回目 | 71.928s | 28.131s |
ただし、このプログラムのキャッシュのキーは配列データの値を文字列連結しただけなのでさらに改良が必要かもしれない。