Pythonではじめてのフーリエ変換・逆フーリエ変換
Pythonではじめてフーリエ変換・逆フーリエ変換を使ってみましたので、その時の忘備録とともに、これからPythonでFFTを使いたい方がこの記事を役立ていただければ幸いです。
Pythonでフーリエ変換を行う場合は、デジタル信号を扱うことになるため離散フーリエ変換(DFT)のアルゴリズムを使うことになります。これを理解するには非常に難しいです。正直私もDFTはよく分かっていません。(^_^;) ですが、仕組みがわからなくてもnumpyのfft関数を使えば誰でもフーリエ変換できますので、ぜひチャレンジしてみてください。
▼ ArduinoやRaspberry Piを使えば、FFTを使ったガジェットを作れます!
はじめに
まず、フーリエ変換は音声データなどで時間領域を周波数領域に変換する数学というかアルゴリズムです。フーリエ変換を行えば、サンプルデータの中にどの周波数がどのくらいの大きさで含まれているかを調べることが簡単にできるようになります。このことを周波数特性と呼びます。
フーリエ変換の知識が無くてもPythonならプログラミングできますが、ある程度の知識は身につけておいたほうが何かにつまづいたときの助けになります。
そこでおすすめの本をご紹介します。
▼ こちらの書籍はPythonでフーリエ解析を学べます。NumPyやmatplotlibの基本を解説し、SciPyを使った応用プログラムまで網羅してます。 とくに、信号処理への応用が学べるので実践的です。
また、こちらの本は、難解なフーリエ変換の数学をとてもわかり易く解説されてます。フーリエ変換を理解する導入としてとても役立ちました。
上記の本の著者は渋谷道雄氏で、同じ方が書かれたこちらの本も大変読みやすいです。合わせて読むとフーリエ変換の理解がだいぶ進みます。
▼ 上記の2冊を読んで、自分なりにフーリエ変換をまとめました。
フーリエ変換・逆フーリエ変換のプログラム
それではPythonでフーリエ変換・逆フーリエ変換のプログラムを行っていきます。プログラム中でやっていることは次のとおりです。
- サンプリング周波数44.1kで1000Hzの正弦波の配列を用意
- 配列をフーリエ変換して、周波数特性をグラフへプロット
- フーリエ変換したデータから逆フーリエ変換して❶の波形を作り出せるかを確認
こちらがそのプログラムです。
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
# 正弦波のデータ作成
f = 1000
rate = 44100
T = np.arange(0, 0.01, 1 / rate)
s = []
for t in T:
v = np.sin(2 * np.pi * f * t)
s.append(v)
plt.plot(T, s)
plt.xlabel('Time')
plt.ylabel('Gain')
plt.show()
# フーリエ変換
fft_data = np.abs(np.fft.rfft(s))
freqList = np.fft.rfftfreq(len(s), 1.0 / rate) # 横軸
plt.loglog(freqList, 10 * np.log(fft_data))
plt.xlabel('Frequency')
plt.ylabel('Power')
plt.show()
# 逆フーリエ変換
r = np.fft.irfft(fft_data, len(T))
plt.plot(T, r)
plt.xlabel('Time')
plt.ylabel('Gain')
plt.show()プログラムの解説
先ほどのプログラムの内容を詳しくみていきましょう。
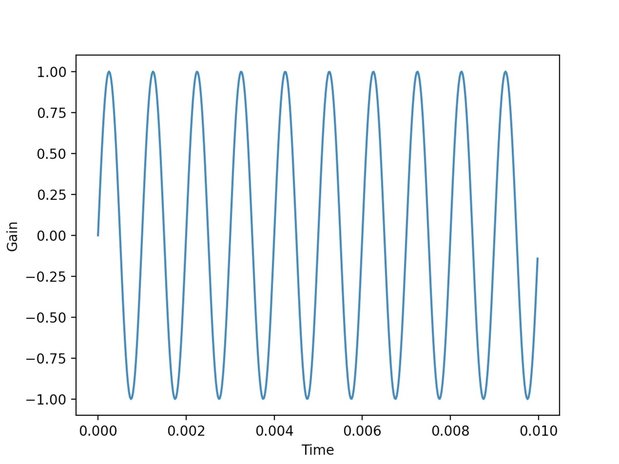
1000Hzの正弦波データ
f = 442
rate = 44100
T = np.arange(0, 0.01, 1 / rate)
s = []
for t in T:
v = np.sin(2 * np.pi * f * t)
s.append(v)フーリエ変換で周波数特性
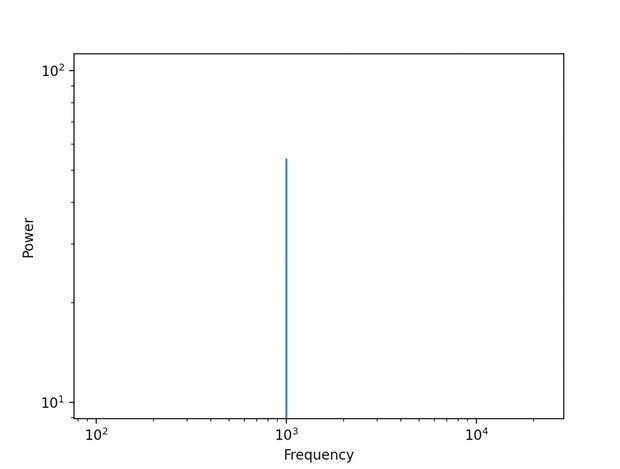
フーリエ変換を行うと実数と虚数のデータの2つが得られますが、虚数データは必要ありません。 ですのでnp.fft.rfftを使って実数データのみを取得してます。 また、グラフの横軸を周波数にしたいので、np.fft.fftfreq(サンプル数, サンプリング周期)で周波数軸のリストを作成しました。 そして、音の振幅をdBに直すため10 * np.log(fft_data)で対数変換を行ないます。
fft_data = np.abs(np.fft.rfft(s))
freqList = np.fft.rfftfreq(len(s), 1.0 / rate) # 横軸こちらのグラフのように、1kHzの周波数成分だけを含むことが確認できました。元の信号の周波数と一致しましたね。
逆フーリエ変換で元の波形を再現
ここでは、フーリエ変換されたデータを元に逆フーリエ変換してます。
r = np.fft.irfft(fft_data, len(T))すると元のデータと同じ数の山を持った、つまり同じ周波数で同じ振幅の波形を作り出すことができました。
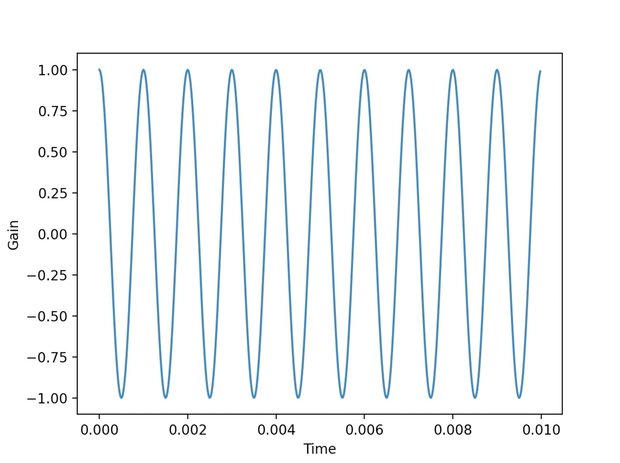
ただし、位相は考慮されていないため余弦波となってしまいました。フーリエ変換では周波数位相特性も調べることができるので、それを使えば元の位相と同じ波形を作れそうです。 ところで、人間の耳は音の位相に鈍感です。余弦波も正弦波も同じ周波数であれば区別が付きません。同じ音色に聞こえても、まったく違う波形になることもあるのです。
ピアノの音をフーリエ変換してみた
ここからは、興味本位でさらに実験を進めてみました。 次のリンクにありますように、ピアノのA音をwavファイルで用意し、Pythonでフーリエ変換してみました。 基音Aのピアノ音
import numpy as np
import matplotlib.pyplot as plt
import wave
from scipy.io.wavfile import write
def load_wav(filename, N):
with wave.open(filename, 'r') as wav:
fr = wav.getframerate()
data = wav.readframes(N)
s = np.frombuffer(data, dtype=np.int16)
return s, fr
def output_wav(filename, rate, data):
write(filename, rate, data.astype(np.int16))
if __name__ == '__main__':
N = 44100
s, rate = load_wav('piano_a.wav', N)
T = np.arange(0, N / rate, 1 / rate)
plt.plot(T, s)
plt.xlabel('Time')
plt.ylabel('Gain')
plt.show()
# フーリエ変換
fft_data = np.abs(np.fft.rfft(s))
freqList = np.fft.rfftfreq(len(s), 1.0 / rate) # 横軸
plt.loglog(freqList, 10 * np.log(fft_data), '.-')
plt.xlabel('Frequency')
plt.ylabel('Power')
plt.show()
# 逆フーリエ変換
r = np.fft.irfft(fft_data, len(T))
plt.plot(T, r)
plt.xlabel('Time')
plt.ylabel('Gain')
plt.show()
output_wav('piano_a_irfft.wav', rate, r)ピアノ音の波形
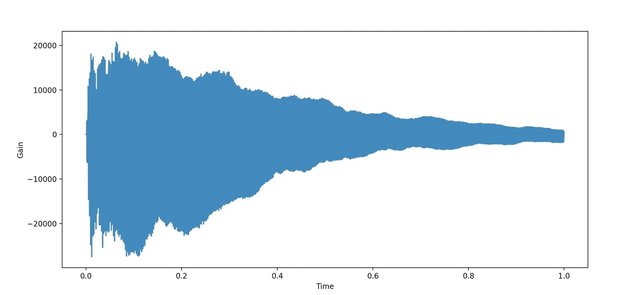
ピアノ音をフーリエ変換
ピアノ音をフーリエ変換して周波数特性を調べてみます。ただし、音源の1秒間だけをサンプルしてフーリエ変換してます。
周波数特性をグラフにすると次のとおりです。
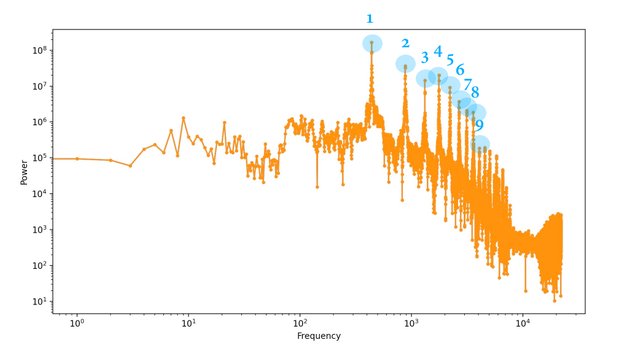
ここで、基音のA音が440Hzにあり、そこから倍音が2倍、3倍と続いているのがグラフから確認できます。また、8倍音あたりまでは計算通りの周波数で倍音があらわれますが、9倍音以降になると大きくズレてきます。9倍音から大きくゲインが下がっているのも気になります。もしかしてこれはピアノの弦とは別の倍音なのでしょうか?
先ほどの周波数特性をグラフにして整理してみます。
| 倍音 | 理論値(Hz) | 目分量で実測(Hz) |
|---|---|---|
| 1 | 440 | 440 |
| 2 | 880 | 880 |
| 3 | 1320 | 1308 |
| 4 | 1760 | 1784 |
| 5 | 2200 | 2200 |
| 6 | 2640 | 2695 |
| 7 | 3080 | 3138 |
| 8 | 3520 | 3563 |
| 9 | 3960 | 4122 |
| 10 | 4400 | 4650 |
| 11 | 4840 | 5115 |
| 12 | 5280 | 5956 |
| 13 | 5720 | 6634 |

逆フーリエ変換して元のピアノ音を作れるか?
「フーリエ変換したデータから逆フーリエ変換して元のピアノ音を作れるだろうか?」 非常に興味のあるテーマでした。さっそくやってみました。逆フーリエ変換した結果がこちらです。
残念ながらというか、予想通りというか、元の波形から随分と異なる波形が生まれました。しかし、こちらの音をぜひ聞いてもらいたいです。逆フーリエ変換したデータをWAVファイルに書き出したものになります。 フーリエ変換→逆フーリエ変換されたピアノ音
音割れは目をつぶってもらって、前半部分だけ聴くとなんとピアノの雰囲気を感じ取れませんでしょうか?少なくとも音程はバッチリなようです。 この結果には正直驚きました。ぜひもう一度、最初のピアノ音源と比較してみてください。
基音Aのピアノ音 フーリエ変換→逆フーリエ変換されたピアノ音
そもそも「周波数成分が時間的変化する音源を、単純な逆フーリエ変換で再現することは不可能」と疑ってかかった実験でしたが、予想外の良い結果でした。何でもやってみるものですね! サンプリング時間をもっと微小時間にしてそれぞれをつなぎ合わせれば、つまり積分のような考え方でつなぎ合わせれば、もっと精度良く原音を復元できそうですね。どなたかやってみますか?
▼ デジタルの信号処理を詳しく勉強したい方はこちらの書籍がおすすめです。高速フーリエ変換(FFT)や離散フーリエ変換(DFT)の仕組みから、IIRやFIRなどのデジタルフィルタが学べます。数学やC言語がメインなので難易度は高めですが、サンプルプログラムが豊富で実践しながら勉強できます。
これらのデジタル信号処理を勉強後、デジタルフィルタを使って「波動」というシンセサイザーアプリを作ってみました。
波動 - Hysteric Oscillator ver1.0.0 - YouTube