伝達関数から周波数応答(周波数振幅特性と周波数位相特性)
前回の記事では、RCローパスフィルタの伝達関数を計算し、ステップ応答を調べるところまでを行なった。__今回はその続きとして、RCローパスフィルタの伝達関数を使って周波数応答(周波数振幅特性と周波数位相特性)を調べてみよう。__
前回の記事はこちら。
Pythonで伝達関数などを扱うにあたっては、こちらの書籍を大いに参考させてもらった。__計算が複雑になりがちな制御工学の伝達関数なども、Pythonでらくらくシミュレーションできるようになるのでおすすめだ。__
はじめに
ステップ応答やインパルス応答などの過渡応答特性は時間関数f(t)の形であるが、周波数特性の場合は、\(s\)の代わりに\(jω\)となる。jは虚数(\(j^2 = -1\))であり、ωは角周波数である\(ω=2πf\)。
実は伝達関数\(G(s)\)の代わりに\(G(jω)\)とすることで周波数振幅特性を調べることができる。また、\(arg(G(jω))\)とすることで周波数位相特性を調べることができる。
周波数振幅特性とは、さまざまな周波数の正弦波をシステムへ入力にした時、どの程度の振幅で出力されるか調べたものである。たとえばシステムが単純なローパスフィルタなら、高周波になるほど出力は小さくるだろう。
また、周波数位相特性とは、さまざまな周波数の正弦波をシステムへ入力にした時、どの程度の入力の位相とずれているかを調べたものである。
これらのことが\(G(jω)\)や\(arg(G(jω))\)で調べられるわけだが、なぜ\(s=jω\)とするのかの理由はフーリエ変換やオイラーの公式を使って説明されるため非常に難しので本記事では省略する。しかし、理屈を知らなくても伝達関数さえ分かっていれば簡単に周波数特性を調べられるので、本記事ではとにかく実践を大事に周波数応答の実験をしてみたいと思う。
具体的にはPythonでプログラミングして周波数特性をグラフ化していく。
周波数応答
さて、RCローパスフィルタの伝達関数は次の通りであった。
$$G(s)=\frac{1}{1+RCs}$$よって、周波数振幅特性を調べるためには
$$G(jω)=\frac{1}{1+jωRC}$$とすれば良いことになる。
また、周波数位相特性を調べるためには\(arg(G(jω))\)であった。argとは複素数平面上での偏角のことである。
さて、\(ω=2πf\)であるので調べたい周波数\(f\)を変えて計算すれば良いわけだが、周波数は膨大にあるため手動で計算するのはほぼ不可能だ。そこでPythonを使って周波数応答をグラフ化していく。
次のプログラムは抵抗R=1kΩ、コンデンサの容量を1μF、入力のサイン波の電圧を1としたときの周波数応答をグラフ化させるプログラムである。
from control.matlab import *
import matplotlib.pyplot as plt
if __name__ == '__main__':
R = 1 * pow(10, 3) # 1kΩ
C = 1 * pow(10, -6) # 1μF
K = 1 # ゲイン
T = R * C # 時定数
G = tf([0, K], [T, 1]) # 伝達関数
W = logspace(1, 5) # 対数スケールの配列
gain, phase, w = bode(G, W, Hz=True)
plt.show()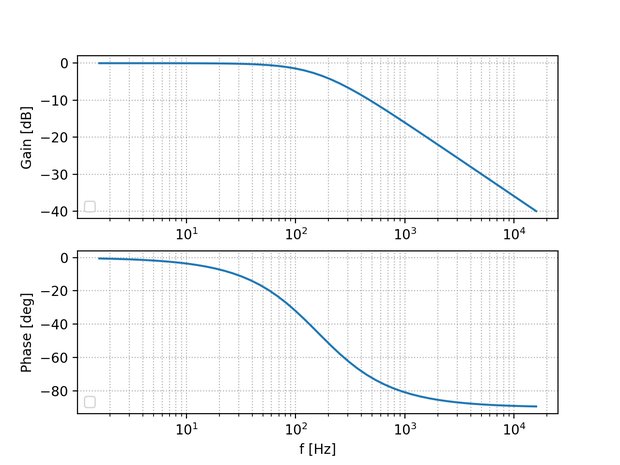
プログラムの説明
ここで、先ほどのプログラムをもう少し詳しく解説する。
伝達関数tfに関しては、以前の記事で詳しく説明したのでここでは省略する。
調べたい周波数領域の設定はlogspaceで行う。これは対数スケールで配列を生成してくれる関数である。今回は100kHzまで調べるので次のように指定した。
W = logspace(1, 5) # 周波数領域[rad/s]の指数また、bode関数を使うことでボード線図のデータを得ることができる。ボード線図とは、周波数振幅特性と周波数位相特性をグラフにプロットしたものである。 bode関数自体にプロットしてグラフ表示する機能が備わっているので返り値は使っていない。またデフォルトでは横軸が角周波数で表示されてしまうので、Hzで表示するように指定した。
gain, phase, w = bode(G, W, Hz=True)カットオフ周波数
次に、RCローパスフィルタのカットオフ周波数について考えてみたい。RCローパスフィルタのカットオフ周波数は次の数式で計算される。
$$f_c=\frac{1}{2πRC}$$カットオフ周波数は振幅が-3dBとなる周波数であるので、R=1kΩ、C=1μFより計算すると約159Hzである。 先ほどのグラフをみても、159Hzあたりでゲインが-3dBになっていることが確認できる。
また、Pythonではシステム(伝達関数)へ正弦波を入力してその応答を確かめることもできる。lsim関数を使うことでそれが可能だ。
y, t, X0 = lsim(sys, Ud, Td, X0)sysは伝達関数モデルや状態空間モデル、Udは入力、Tdは時間、X0が初期値である。また返り値のyが出力、tが時間、X0が初期値である。
下のプログラムでは、RCローパスフィルタのシステムにカットオフ周波数である159Hzの正弦波を入力したときの応答を調べている。
from control.matlab import *
import matplotlib.pyplot as plt
import numpy as np
if __name__ == '__main__':
R = 1 * pow(10, 3) # 1kΩ
C = 1 * pow(10, -6) # 1μF
K = 1 # ゲイン
T = R * C # 時定数
w = 2 * np.pi * 159
G = tf([0, K], [T, 1]) # 伝達関数
Td = np.arange(0, 0.05, 0.0001)
u = np.sin(w*Td)
y, t, X0 = lsim(G, u, Td, 0)
plt.plot(t, u, label='u(t)')
plt.plot(t, y, label='y(t)')
plt.legend()
plt.show()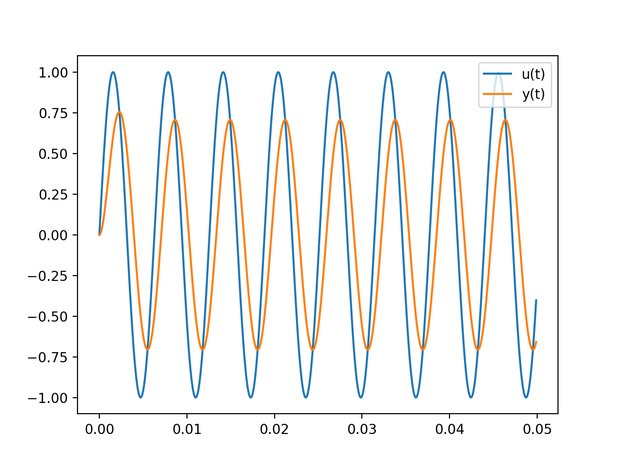
となり、159Hzがカットオフ周波数であることを確かめられた。
サウンドプログラミングの参考書
さいごに、私がよく参考しているサウンドプログラミングの書籍を紹介しておく。これらの本を熟読すれば、デジタルフィルタの面白さ、魅力がたのしめ、デジタル信号の解析方法への理解は深まると思う。ぜひ参考に。


















