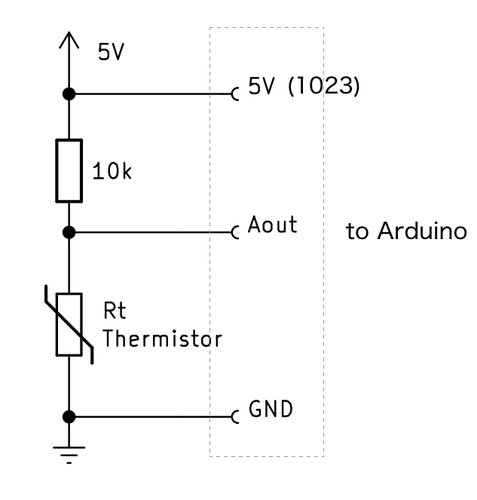
Arduinoとサーミスタで温度測定
こんなこと、やります。
- サーミスタの使い方、計算方法を学ぶ
- Arduinoとサーミスタを使って温度の測定
- サーミスタの温度校正
つかうもの
本記事でつかうものをご紹介します。
サーミスタ
103JT-050というサーミスタを使用しました。薄型である程度曲げることができます。
厚さは500μmと超薄型で、電気絶縁性も優れてます。 温度測定範囲は、-50℃〜+125℃となってます。Arduino
Arduino Uno Rev3を使用しました。
もちろん他のArduinoでも構いません。
もしまだArduinoをお持ちでないようでしたら、 おすすめArduinoどれを選べばいい?Arduinoで電子工作をはじめる方へ をご覧ください。
その他の電子部品
プルアップのため10kΩの固定抵抗を使います。プルアップ抵抗の誤差は温度計算に影響しますので、誤差範囲の小さい抵抗を選んでください。金属皮膜抵抗ですと±1%以内でおすすめです。また、ブレッドボードやジャンプワイヤもあると便利です。
サーミスタ
ここではサーミスタについて解説します。
サーミスタとは
サーミスタとは、温度変化にともなって抵抗値が変化する抵抗器です。温度のthermalと抵抗器のresistorを合わせ、サーミスタという名称になりました。 温度センサに使用されるサーミスタは、NTC(negative temperature coefficient)といって、温度が上昇すると抵抗値が減少するタイプのものです。 温度が上昇すると抵抗値が上昇するものは、PTC(positive temperature coefficient)と呼び、ヒューズの役割として使ったり、一定温度を保つPTCヒーターに利用されます。
ちなみにこちらのPTCヒーターを使ってヨーグルトメーカーをつくったことがあります。興味のある方は そうだ!Arduinoでヨーグルトメーカーをつくろう! をご覧ください。
本記事では、温度センサとしてよく使われるNTCタイプのサーミスタを扱います。
NTCサーミスタの特性・近似式
サーミスタは、温度変化に対して抵抗値が変わる素子であることは説明しました。しかし、サーミスタと温度と抵抗の関係は非線形です。よって、サーミスタの抵抗値から温度を得るためには、NTCサーミスタの特性を近似させた次式を利用します。
$$R=R_0exp\{B(\frac{1}{T}-\frac{1}{T_0})\} \tag{1}$$ここで、BはB定数と呼ばれるもので、サーミスタのデータシートに掲載されてます。
また、Tの単位はケルビンになります。摂氏温度を取得するには次式で変換します。
$$T(K)=t(℃)+273.15 \tag{2}$$さて、式1をTについて展開すると次のとおりです。
$$\frac{1}{T} = \frac{1}{T_0}+\frac{1}{B}ln\frac{R}{R_0} \tag{3}$$式3の逆数をとれば、Tについて算出できます。
さらに高精度で近似させる「スタインハート式」というものがありますが、式3でも実用的な温度測定ができますので「スタインハート式」については省略します。
\スタインハート式を使った校正/
必要なパラメータ(103JT-050)
サーミスタで温度測定に必要なパラメータを確認します。今回使用するサーミスタは103JT-050ですので、 データシート より各パラメータは次のとおりになります。
| 項目 | 値 | 備考 |
|---|---|---|
| B定数 | 3435K | ±1%(25℃の時) |
| \(T_0\) | 273.15K | 0℃の時 |
| \(R_0\) | 27.7kΩ | 0℃の時 |
| \(R_{25}\) | 10kΩ | ±1%(25℃の時) |
抵抗・温度特性のシミュレーション
サーミスタ103JT-050の データシート から、理論値をプロットしてみました。また、式1の近似式と103JT-050のパラメータから抵抗値を計算し、抵抗と温度特性のシミュレーションをしてみました。
次のグラフは、サーミスタ103JTの抵抗・温度特性における、理論値と近似値の関係を表したものです。
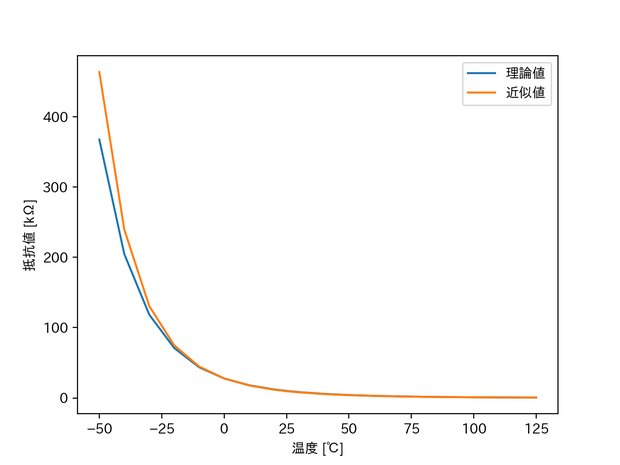
さらに、0℃以上に絞ってみてみます。すると下図のとおり、かなり高い精度で近似できることが分かりました。
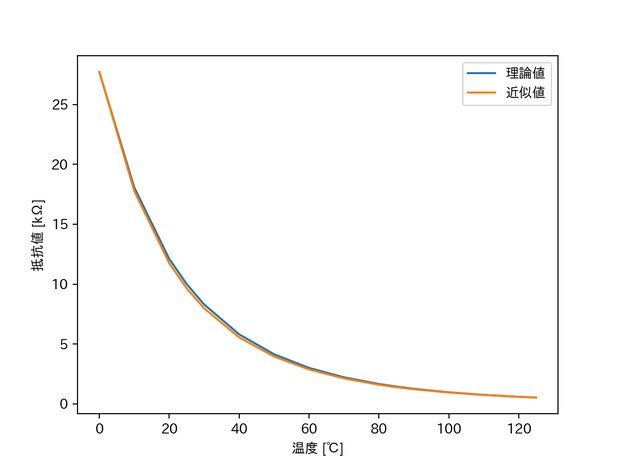
Pythonのソースコード
さきほどのグラフを作ったPythonのソースコードです。このプログラムを少し修正すれば、Raspberry Piでサーミスタを使う場合にも利用できます。
# -*- coding: utf-8 -*-
import math
import matplotlib.pyplot as plt
import japanize_matplotlib
"""
サーミスタ103JTの抵抗ー温度特性
抵抗値はkΩ
"""
list_temp = [-50, -40, -30, -20, -10, 0, 10, 20, 25, 30, 40, 50, 60, 70, 80,
85, 90, 100, 110, 120, 125]
list_R = [367.7, 204.7, 118.5, 71.02, 43.67, 27.70, 18.07, 12.11, 10.00, 8.301,
5.811, 4.147, 3.011, 2.224, 1.668, 1.451, 1.267, 0.9753, 0.7597, 0.5981, 0.5331]
T0 = 273.15
R0 = 27.70
B = 3435
list_r = [R0 * math.exp(B*(1/(t+273.15)-1/T0)) for t in list_temp] # [条件式 for 変数名 in リストなど]
def plot(t, R, r): # t温度、R理論値、r近似値
fig, ax = plt.subplots(facecolor="w")
plt.xlabel('温度 [℃]')
plt.ylabel('抵抗値 [kΩ]')
ax.plot(list_temp, list_R)
ax.plot(list_temp, list_r)
ax.legend(["理論値", "近似値"])
plt.show()
plot(list_temp, list_R, list_r)
# 0℃以上のデータのみ
del list_temp[:5]
del list_R[:5]
del list_r[:5]
plot(list_temp, list_R, list_r)Arduinoでサーミスタを使う
実際にArduinoでサーミスタを使っていきましょう。
Arduinoとサーミスタの配線
こちらの図のように、Arduinoとサーミスタを配線します。
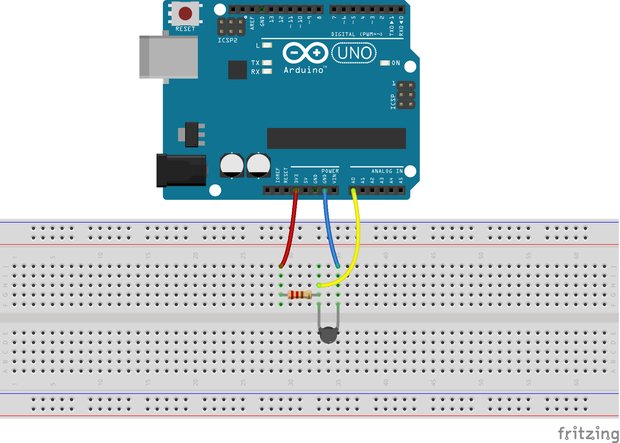
サーミスタと固定抵抗で分圧した値を、Arduinoのアナログ入力で読み取り、サーミスタの抵抗値を算出します。 サーミスタ103JT-050では、25℃のときに10kΩの抵抗値になりますので、固定抵抗を10kΩとしました。ここらへんは、測定したい温度範囲によって変えてもらって構いません。また、固定抵抗にはできるだけ誤差の少ない金属皮膜抵抗を使用しましょう。 センサにかける電圧は5Vを使用しました。
サーミスタで温度測定するソースコード
こちらが、Arduinoとサーミスタを使って温度を測定するソースコードになります。
#include <math.h>
#define THERMISTOR_PIN 0
const float DIVIDER = 10000.0; // 分圧抵抗10kΩ
const float T0 = 273.15;
const float R0 = 27700.0;
const float B = 3435.0;
float calcTemp(float Rt) {
float T_bar = 1/T0 + 1/B * log(Rt/R0);
return 1.0/T_bar - 273.15;
}
void setup() {
Serial.begin(9600);
pinMode(THERMISTOR_PIN, INPUT);
}
void loop() {
float Aout = float(analogRead(THERMISTOR_PIN));
// Serial.println(Aout);
float Rt = DIVIDER * Aout / (1024.0 - Aout);
float temp = calcTemp(Rt);
Serial.println(temp);
delay(1000);
}ソースコードの解説
サーミスタの抵抗値Rtの算出
loop関数内では、アナログ入力値からサーミスタの抵抗値を算出してます。抵抗値とADCの値の比を考えると、次式のようになります。
$$Aout:1024-Aout = R_t:10k \tag{4}$$式4より、Rtについて解くと次式となります。
$$R_t=\frac{10k \times Aout}{1024-Aout} \tag{5}$$居酒屋ガレージ日記さん にご指摘いただきまして、1023で割っていた式を1024に修正させていただきます。そもそもADコンバータで測れる値は、
$$V_{ref} - 1LSB = V_{ref} (1 - 1/1024)$$という事らしいです。ですから厳密には、図中の5Vを\(V_{ref} - 1LSB\)にするのが正解なような気がします。
近似値の計算
calcTemp関数では、式3の近似値の計算式をそのままプログラミングしてます。サーミスタと分圧抵抗をステレオミニにまとめてはんだ付けしました。VccをTip、AoutをRing、GNDをSleeveに割り当ててます。

サーミスタの温度誤差について
さて、ここまでの回路とプログラムを組んでサーミスタで温度測定してみると、製品の温度計と照らし合わせた時に温度がだいぶズレてしまいます。理論値はあくまで机上のものであることが分かります。そこでサーミスタの温度校正が必要になります。 温度が理論値からズレてしまう要因としましては、ADコンバータの精度、サーミスタの精度、基準となる製品の温度計の信頼性、温度観測ポイントのムラなどが挙げられます。ADコンバータのVref電圧にも気を使わないと、ArduinoやESP32などの内蔵ADコンバータで精度高く測定するのは難しいです。
そこで、サーミスタの温度精度をより上げるには、3点温度の抵抗値を測定してスタインハート式を使った温度校正をおすすめします。
スタインハート式を使ったサーミスタの温度校正のやり方
難しい理屈は分からなくても、3温度試験点の抵抗値が分かれば校正できますので恐れずに試してみてください^^ スタインハート式で温度校正することで、基準温度計とほぼ同じ値を表示させることが可能になります。
基準温度計
3温度試験点を測定するために、基準となる温度計が必要です。もちろん基準温度計が狂っていたら元も子もありませんが、料理などで使える温度計は比較的信頼できます。なぜなら、水の沸点は100℃、氷水の温度は0℃であることを確かめることができるからです。
スタインハート式
$${\displaystyle {\frac {1}{T}}=A+B\ln R_t+C(\ln R_t)^{3}}$$A、B、Cは3点温度の抵抗値より決定される定数です。また、Rtはその瞬間のサーミスタの抵抗値[Ω]、Tは温度[K(ケルビン)]です。
ただし、定数A、B、Cを計算するために、かなりややこしい計算が必要になります。ここでは サーミスタのSteinhart-Hartパラメータ算出 のサイトを利用させてもらい、3点の温度と抵抗値だけを入力して定数A、B、Cを算出しました。より詳しい数式を知りたい方は、 Steinhart–Hart equation (英語版のWikipedia) をご覧ください。
3温度試験点での抵抗値の測定方法
測定した3点の温度と抵抗値を、 サーミスタのSteinhart-Hartパラメータ算出 のサイトで入力して定数A、B、Cを算出してください。3点の温度は、氷水、水道水(または常温の水)、沸騰したお湯を使うと便利です。
また抵抗値の測定は、テスターを使わずにESP32のADコンバータからプログラミングによって導き出します。そうすることで、ADコンバータや抵抗値の精度をある程度緩和する狙いがあります。次の写真は、スタインハート式を使って校正された温度測定の様子です。ご覧の通り、基準温度計とほぼ同じ値を示すように校正できました。
▼ こちらはDHT22やThermoProの室内温度計と照らし合わせながらチェックしている様子です。サーミスタの校正がここまで精度高くなると、今度はDHT22の温度校正の方が問題になってきました^^;

103AT-11の実測値
例として、サーミスタ103AT-11とESP32を使って温度3点における抵抗値の測定結果を記します。
| 温度[℃] | 抵抗値[Ω] |
|---|---|
| 0.8 | 20000.00 |
| 11.2 | 13430.0 |
| 101.8 | 534.0 |
これより、定数は次のとおり導き出されました。
| 定数 | 値 |
|---|---|
| A | 0.00173842581 |
| B | 0.00011745478 |
| C | 0.00000077076524 |
スタインハート式を使った温度測定のソースコード
スタインハート式を使った温度測定のソースコードの一部をご紹介いたします。Arduino言語(C++)で動きます。ESP32のための関数なので、ADコンバータの分解能に注意してください。Arduino Unoなどで使う場合は、4096.0 を 1024.0 へ置き換えてください。
float calcTemp() {
float divider = 10000.0; // 分圧抵抗10kΩ
float aout = float(analogRead(SENSOR_PIN));
float OFFSET_RT = 0;
float Rt = OFFSET_RT + divider * aout / (4096.0 - aout);
Serial.print("Rt: ");
Serial.println(Rt);
/**
* @brief 103AT-11の実測値
* 0.8*C = 20000.00 (103AT-11)
* 11.2*C = 13430.0 (103AT-11)
* 101.8*C = 534 (103AT-11)
*/
float THERM_T0 = 273.15;
float THERM_R0 = 27280.0;
float THERM_A = 0.00173842581;
float THERM_B = 0.00011745478;
float THERM_C = 0.00000077076524;
float T_bar = THERM_A + THERM_B * log(Rt) + THERM_C * pow(log(Rt), 3);
return 1.0 / T_bar - 273.15;
}スタインハート式を使って校正されたサーミスタの温度測定の動画
動画はYouTubeの アイデアノート channel で公開中です。